Question

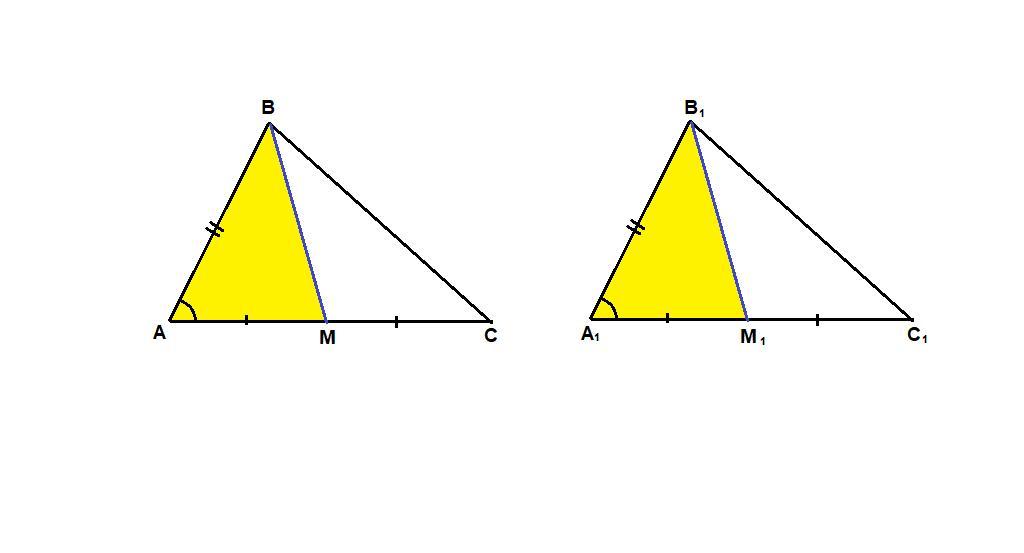
Докажите, что медианы, проведенные к равным сторонам равных треугольников, равны.

Answer 1

Допустим, ети треугольники - АБЦ и НКТ.Медиана в етом случае у первого треуг. БС, а во втором треуг. КД. Если треугольники равны, то АЦ =НТ, угол БАС = углу КНД, угол АБЦ равен углу НКТ. Сейчас доведем, что треугольник АБС равен треуг. НКД: АБ равна НК, угол БАС равен углу КНД, угол АБС равен углу НКД. Вывод: угол Абс равен углу НКД как половины к равным углам. Треугольник АБС и треуг. НКД равны. Тогда и БС равна КД. Пожалуйста)))

Answer 2

Ответ:

Дано: ΔАВС = ΔА₁В₁С₁, ВМ и В₁М₁ - медианы.

Доказать: ВМ = В₁М₁.

Доказательство:

АВ = А₁В₁ как соответствующие стороны равных треугольников,

∠А = ∠А₁ как соответствующие углы равных треугольников,

АМ = 1/2 АС        А₁М₁ = 1/2 А₁С₁,  а так как АС = А₁С₁, то и

АМ = А₁М₁, значит

ΔАВМ = ΔА₁В₁М₁ по двум сторонам и углу между ними.

В равных треугольниках напротив равных углов лежат равные стороны, значит ВМ = В₁М₁.