Question

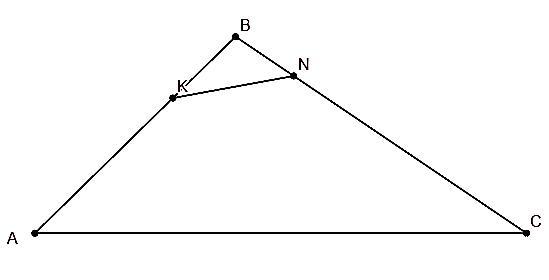
Прямая пересекает стороны АВ и ВС треугольника АВС в точках К и N соответственно. Известно, что AB= CN = 16, ВС=20, AC= 28, AK= 11. Найдите длину отрезка KN.

Answer 1

Раз по условию АК = 11 и CN = 16, то KB = 16 - 11 = 5 и BN = 20 - 16 = 4.

Так как $\dfrac{AB}{BC}=\dfrac{16}{20}=\dfrac{4}{5}=\dfrac{BN}{BK}$ и угол B у треугольников BKN и ABC общий, то ΔABC ~ ΔBKN по двум пропорциональным сторонам и углу между ними. Из подобия треугольников следует пропорциональность соответствующих сторон

$\dfrac{BN}{BC}=\dfrac{KN}{AC}\\ \\ KN=\dfrac{BN\cdot AC}{AB}=\dfrac{4\cdot 28}{16}=7$