Предмет: Алгебра,
автор: музыка
пожалуйста, помогите доказать равенство:
Приложения:
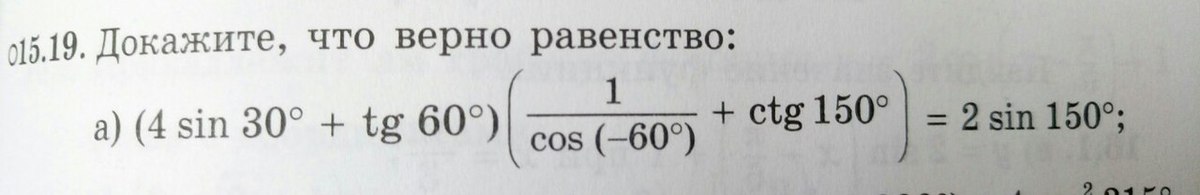
Ответы
Автор ответа:
0
Решение
(4sin30° + tg60°)(1/cos(-60°)) + ctg150°) = 2sin150°
Левая часть:
(4sin30° + tg60°)(1/cos(-60°)) + ctg150°) =
= 4*(1/2) + √3)*(1/(1/2) + ctg(180° - 30°) =
= (2 + √3)*(2 - ctg30°) = (2 + √3)*(2 + √3) = 4 - (√3)² = 4 - 3 = 1
Правая часть:
2sin150° = 2sin(180° - 30°) = 2sin30° = 2*(1/2) = 1
1 = 1
равенство доказано
(4sin30° + tg60°)(1/cos(-60°)) + ctg150°) = 2sin150°
Левая часть:
(4sin30° + tg60°)(1/cos(-60°)) + ctg150°) =
= 4*(1/2) + √3)*(1/(1/2) + ctg(180° - 30°) =
= (2 + √3)*(2 - ctg30°) = (2 + √3)*(2 + √3) = 4 - (√3)² = 4 - 3 = 1
Правая часть:
2sin150° = 2sin(180° - 30°) = 2sin30° = 2*(1/2) = 1
1 = 1
равенство доказано
Похожие вопросы
Предмет: Литература,
автор: ryahencevs
Предмет: Математика,
автор: juriakimu887
Предмет: Алгебра,
автор: ellahvan65
Предмет: Информатика,
автор: обри