Question

помогите пожалуйста!
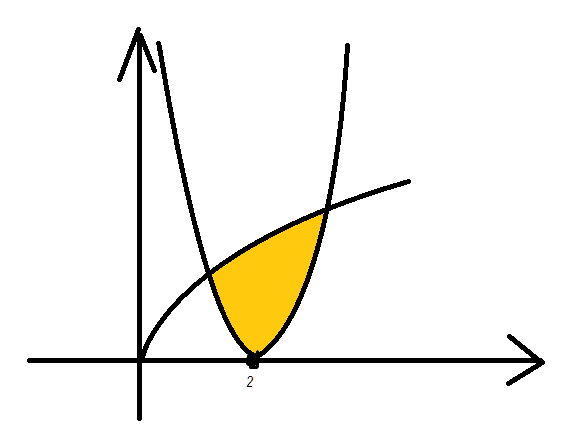
найдите площадь фигуры,ограниченной графиками функций y=корень из x ,y=(x-2)^2 и осью Ох

Answer 1

Построим графики.
Строим график y=√x, точки: (0;0), (1;1), (4;2), (9;3)
А график (x-2)² параллельно перенести график у=х² на 2 еденицы вправо.

Приравняем оба функции
$sqrt{x} =(x-2)^2 \ x=(x-2)^4 \ x^4-8x^3+24x^2-33x+16=0 \ x^3(x-1)-7x^2(x-1)+17x(x-1)-16(x-1)=0 \ (x-1)(x^3-7x^2+17x-16)=0 \ x_1=0 \ x^3-7x^2+17x-16=0$
ПО формуле Кардано $x_2= frac{14+ sqrt[3]{188+12 sqrt{249} }+ sqrt[3]{188-12 sqrt{249} } }{6}$

$S= intlimits^{frac{14+ sqrt[3]{188+12 sqrt{249} }+ sqrt[3]{188-12 sqrt{249} } }{6}}_1 {(-x^2+4x-4+ sqrt{x} )} , dx = \ \ = intlimits^{frac{14+ sqrt[3]{188+12 sqrt{249} }+ sqrt[3]{188-12 sqrt{249} } }{6}}_1 {(- frac{x^3}{3}+2x^2-4x+ frac{2}{3} sqrt{x^3}) } , dx =$

Посчитать х=1 можно а вот с иррациональным совсем трудно(((