Question

ОЧЕНЬ НАДО
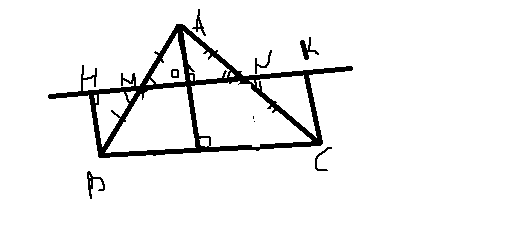
А)Точки M и N- середины сторон АВ и АС остроугольного треугольника АВС, отрезки ВН и СК - перпендикуляры, проведенные из точек В и С к прямой МN. Докажите, что четырехугольник ВСКН и треугольник АВС равносоставлены.
Б) Найдите периметр квадрата с площадью 25 м^2
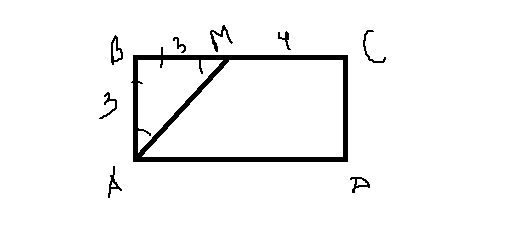
В)Биссектриса угла А прямоугольника АВСD пересекает сторону ВС в точке М. Найдите площадь прямоугольника, если ВМ=3 см и МС=4 см.
Г)Найдите стороны прямоугольника с площадью 14 см^2 и периметром 18 см.

Answer 1

1)треуг ВНМ=МАО и CKN=ANO по гипотенузе и острому углу, значит фигуры равносоставлены (состоят из равных элементов)т(рис 1)
2)сторона √25=5 Р=4*5=20
4)стороны 7 и 2  (х*у=14 х+у=18)
3)площадь равна 3*(3+4)=3*7=21 (рис 2)