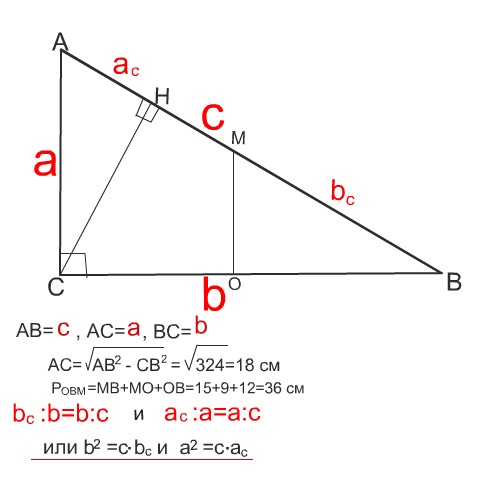
в прямоугольном треугольнике гипотенуза равна 30 см., а один из катетов 24 см. Найдите: а) периметр треугольника, отсекающий от данного меньшей средней линией б) проекции катетов на гипотенузу.
Ответы
По теореме Пифагора второй катет равен
b=18 см
Меньшая средняя линия соотвествует меньшему катету прямоугольного треугольника
Средняя линия треугольника - отрезок соединяющий середины сторон треугольника.
Средняя линия треугольника равна половине соотвествующей стороны
Значит периметр треугольника, отсекающий от данного меньшей средней линией равен
P=(30+24+18):2=36 см
Квадрат длины катета равен произведению гипотенузы на проекцию этого катета на гипотенузу, поэтому проэкции катетов на гипотенузу равны
24^2:30=19,2 см
и 18^2:30=10,8 см
Периметр треугольника, отсекаемого от данного меньшей средней линией, равен полумериметру исходного.
Известны две стороны треугольника.
Третью найдем по теореме Пифагора:
АС= √(АВ²-ВС²)=18 см
Р МВО=(18+24+30):2=36 см
---------------------------------------------
Проекции коротких сторон на длинную делят гипотенузу на два отрезка разной длины.
Для нахождения их воспольземся тем, что Катет - среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу (см.рисунок)
BН=СВ²:АВ=576:30=19,2 см
АН=АС²:АВ=324:30=10,8 см
Проверка:
АН+ВН=19,2+10,8=30 см