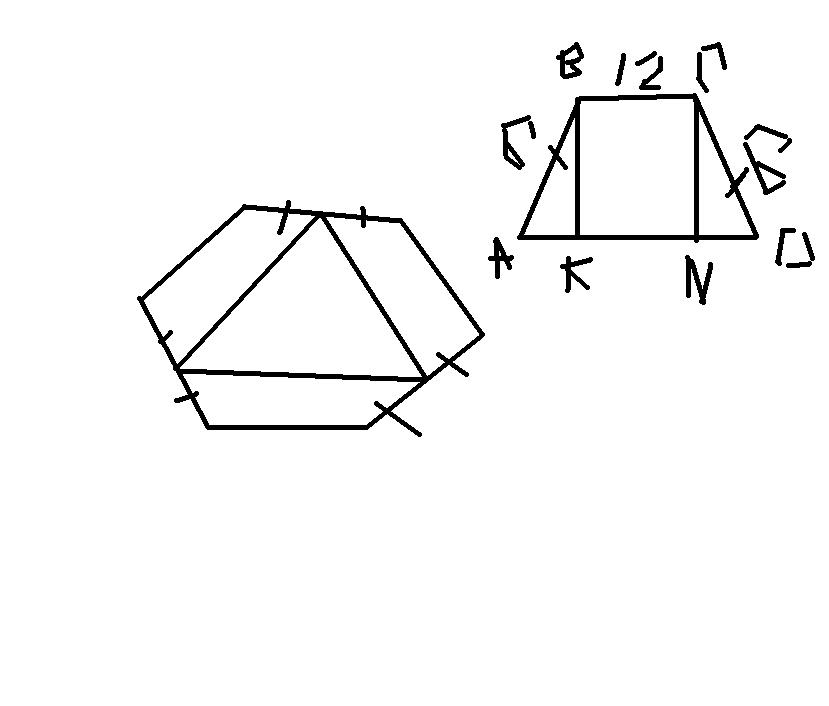
Сторона правильного шестиугольника равна 12 см. Середины трех его сторон ,взятых через одну,есть вершинами треугольника.Найти площадь этого треугольника.
Ответы
Рассмотрим трапецию ABCD, образованную стороной шестиугольника, двумя половина сторон шестиугольника и стороной построенного треугольника (то что этот четырехугольник трапеция следует из теоремы Фалеса и условия, что стороны треугольника соеденият середины шестиугольника)
AB=12 см, AD=BC=AB/2=6 см
проведем высоты BK и CN, тогда
BCNK - прямоугольник, треугольники AKB и DNC прямоугольные и равные
BC=KN=12 cм
угол АВС как внутренний угол правильного шестиугольника равен 120 градусов,отсюда
угол АВК равен 120-90=30 градусов, угол ВАК=90-30=60 градусов
Значит AK=AB*cos 60=AB/2=6/2=3 см
(или по свойству треугольника с углами 90,60, 30)
Значит сторона AD=3+12+3=18 см
Аналогично получаем что две другие стороны треугольника равны 18 см, т.е. полученный построением треугольник правильный
Искомая площадь треугольника как площадь правильного треугольника равна
кв.см