Question

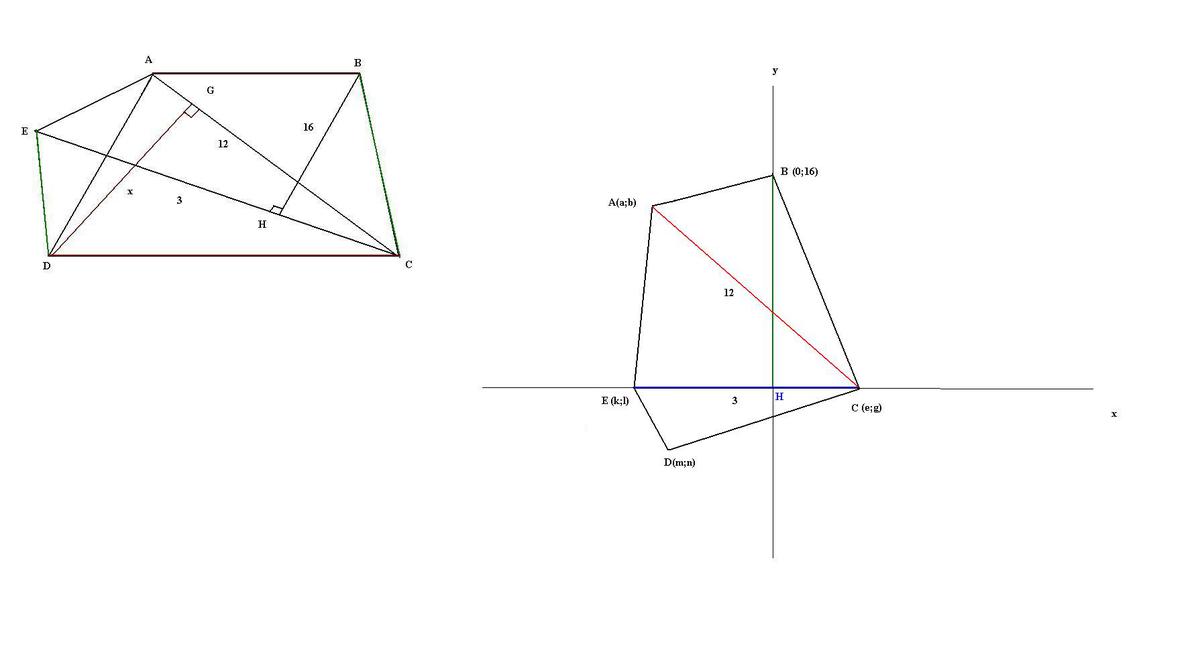
В пятиугольнике,АВ║CД, ДE║BC
АС=12,ЕС=3,от В до ЕС = 16,от Д до АС?

Answer 1

  Предложу аналитическое решение 
Впишем наш пятиугольник в систему координат $OXY$, так чтобы $BH|| OY\ EC|| OX$ , где $BH$ есть расстояние,тогда очевидно координата  $B(0;16)$ ,тогда $E(k;0)\ C(e;0)$ где $e;k$ координаты абсцисс соответствующих точек.    
Обозначим так же координаты $A(a;b)\ D(m;n)$ , и  условимся что 
 $m;n<0\ a<0$ , так как иначе пятиугольник будет не выпуклый, что следует из анализа самой задачи. 
Так как $EC=3\ sqrt{(e-k)^2}=3\ |e-k|=3$
положим что  $e=1\ k=-2$ что верно по условию , так как $e<0$.  То есть сама задача сводится на нахождение такой конструкций пятиугольника, что все компоненты будут верны, иными словами параллельность и длины. 
Так как мы знаем координаты точек  $B(0;16) C(1;0)$ , то его уравнение $BC\ 16x+y-16=0$ по известной формуле по двум точкам. 
уравнение $ED\ -nx+(m+2)y-2n=0$ 
а так как они параллельны , то выполняется условие 
 $-frac{-16}{n}=frac{1}{m+2} neq frac{16}{2n}$ 
Вторую часть 
$AB\ (16-b)x+ay-16a=0\\ DC\ -nx+(m-1)y+n=0$ 
так же  $frac{16-b}{-n}=frac{a}{m-1} neq frac{-16a}{n}$
И выполняется условие 
$(1-a)^2+b^2=144$ то есть это длина отрезка $AC$ . 

из уравнения  
$frac{-16}{n}=frac{1}{m+2}\ n=-16(m+2)$
так как $n<0\ m>-2$ , возьмем  $m=-1$, тогда $n=-16$ , что верно по условию $m,n<0$

Откуда получается система для второй точек координат 
 $-32+2b=16a\ (1-a)^2+b^2=144$
 из решения получаем 
 $a=frac{12sqrt{61}-127}{65}\ b=frac{24(4sqrt{61}+1)}{65}$ 

и все условию будут выполнены 
Теперь по формуле нахождения расстояние от точки до прямой  
уравнение $AC$ 
  $AC\ 2*(4+sqrt{61})+3y-2(4+sqrt{61})=0$ 
 координата точки $D(-1;-16)$ 
 откуда расстояние равно 
 $frac{|-1*2(4+sqrt{61})-3*16 - 2(4+sqrt{61})|}{sqrt{(2(4+sqrt{61}))^2+3^2}}=4$ 
  

Answer 2

ну, а сообразить, что площади треугольников BEC и DAC равны половине площади параллелограмма MBCD, где M - точка пересечения BA и DE - было сложнее, чем эти зубодробительные вычисления?

Answer 3

да я так для разнообразия решил попробовать , когда нарисовал чертеж эти зубодробительные вычисления пришли в голову