Предмет: Математика,
автор: N113
С решением, пожалуйста.
Приложения:
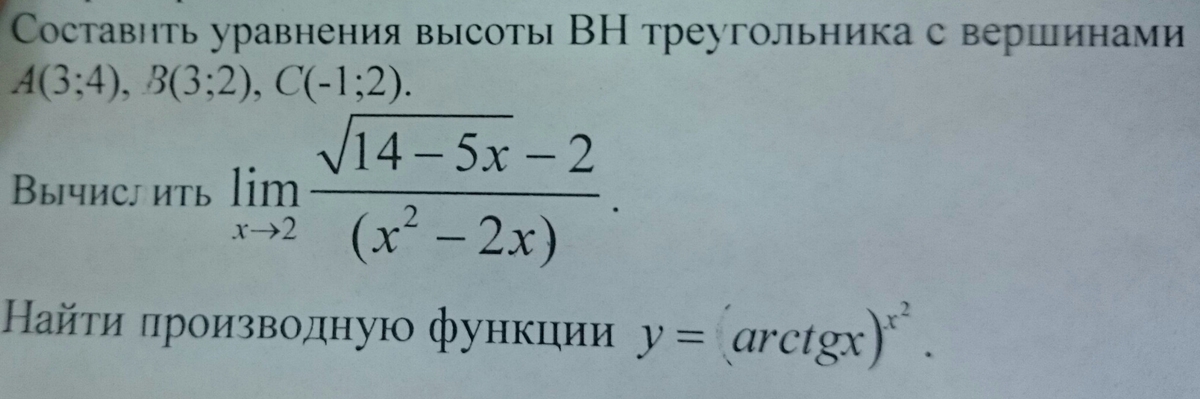
Ответы
Автор ответа:
0
Прямая, проходящая через точку H(x0;y0) и перпендикулярная прямой Ax + By + C = 0 имеет направляющий вектор (A;B) и, значит, представляется уравнениями:
Найдем уравнение высоты через вершину В

Уравнение высоты имеет вид: или
или 
Предел
Если подставить вместо х=2, то в знаменателе получаем 0 и на 0 делить нельзя. Воспользуемся правилом Лопиталя


Найдем уравнение высоты через вершину В
Уравнение высоты имеет вид:
Предел
Если подставить вместо х=2, то в знаменателе получаем 0 и на 0 делить нельзя. Воспользуемся правилом Лопиталя
Автор ответа:
0
Большое спасибо. Как только кнопка будет доступна, отмечу как лучшее
Автор ответа:
0
Спасибо:)
Автор ответа:
0
Как и обещал:)
Похожие вопросы
Предмет: Алгебра,
автор: valeriahaldina1
Предмет: Химия,
автор: dianailcuk0
Предмет: Алгебра,
автор: orlovvnik
Предмет: Математика,
автор: ilonamongush9