Предмет: Алгебра,
автор: kbogdan
lim 2x^2-x^2 поделить на 4-х^2 (когда Х устремляеться к 2-м)
Приложения:
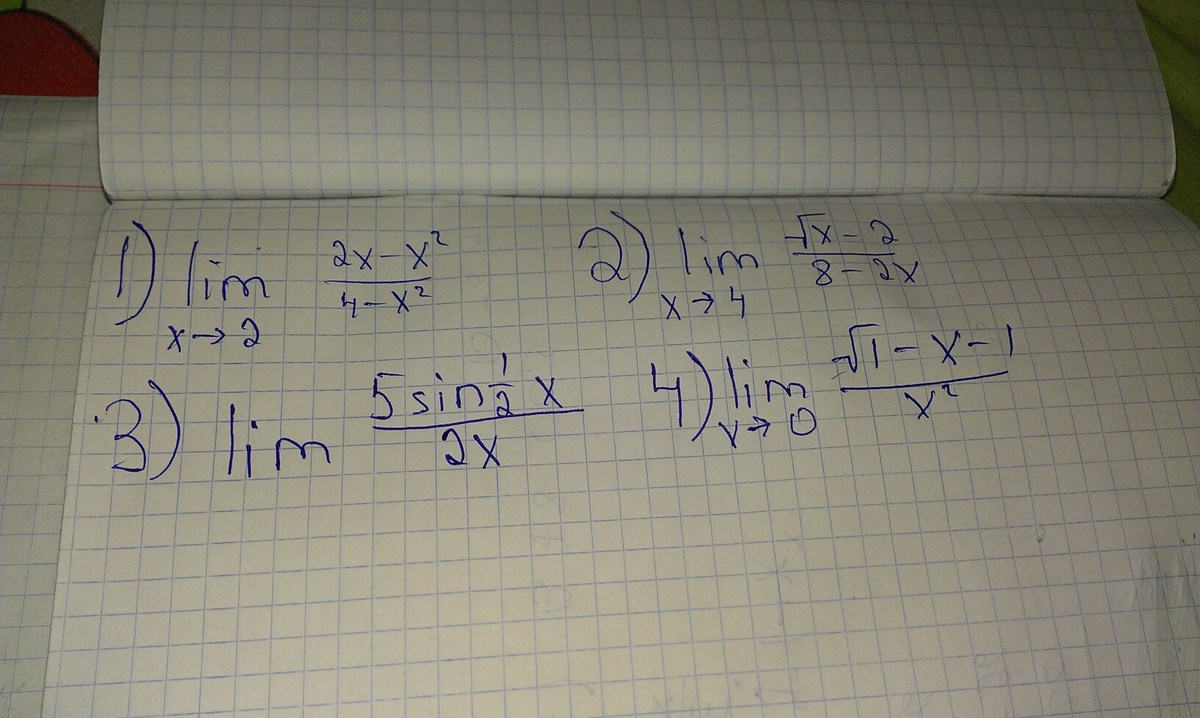
Ответы
Автор ответа:
0
lim_{x->2} (2x-x^2)/(4-x^2) = lim_{x->2} x(2-x)/((2+x)(2-x)) = lim_{x->2} x/(2+x) = 2/(2+2) = 1/2,
lim_{x->4} (√x-2)/(8-2x) = lim_{x->4} (√x-2)/(-2(x-4)) = lim_{x->4} (√x-2)/(-2(√x+2)(√x-2)) = lim_{x->4} -1/(2(√x+2)) = -1/(2(√4+2) = -1/8;
lim_{x->0} (√1-x-1)/x^2 = lim_{x->0} -x/x^2 = lim_{x->0} -1/x = -∞,
lim_{x->0} 5sin(x/2)/(2x) = lim_{x->0} 5sin(x/2)/(4*x/2) = 5/4 lim_{x->0} sin(x/2)/(x/2) =5/4 *1 = 5/4.
Автор ответа:
0
вложение
здесь не указано (предположил что x->0 - что дает повод обратиться к одной из замечательных границ)
Похожие вопросы
Предмет: Русский язык,
автор: olechka0384
Предмет: География,
автор: elakadenko
Предмет: Русский язык,
автор: kostylina52
Предмет: Алгебра,
автор: AppleJargonelle
Предмет: Математика,
автор: stasysuper