Предмет: Алгебра,
автор: koparionlain
Область допустимых значений равно
9^x+16^x-9*4^x+8>0
надо ли его решать
Приложения:
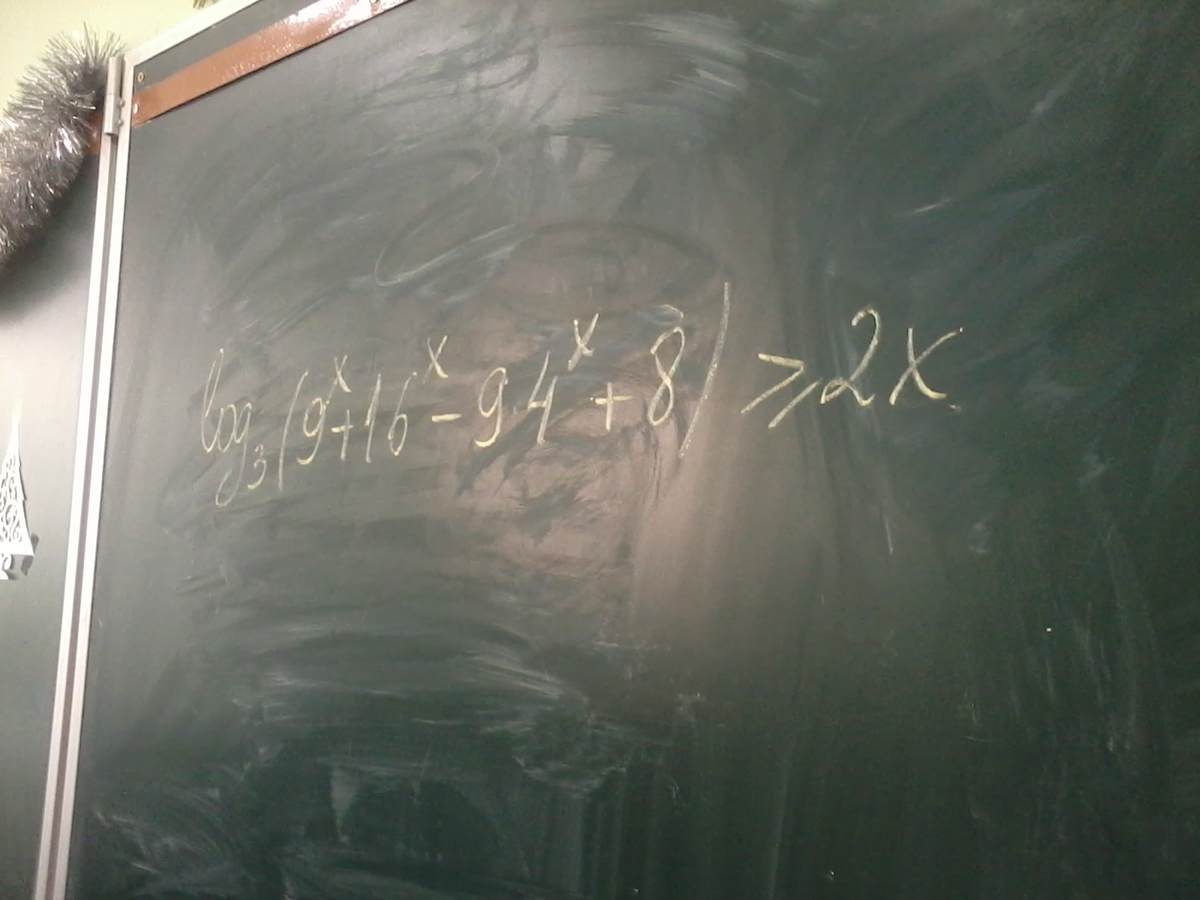
Ответы
Автор ответа:
0
Справа припишем
Применяем формулу логарифма степени к выражению справа:
Логарифмическая функция с основанием 3 - возрастающая, большему значению функции соответствует большее значение аргумента, поэтому
Так как
то неравенство
выполняется и подавно, если выполняется неравенство
Решаем последнее неравенство.
Квадратное неравенство, решаем заменой переменной
t²-9t+8≥0
D=(-9)²-4·8=81-32=49=7²
Корни квадратного трехчлена t²-9t+8
t=(9-7)/2=1 или t=(9+7)/2=8
\\\\\\ //////////////////////
---------[1]---------------[8]---------------
t≤1 или t≥8
Возвращаемся к переменной х:
или
Ответ. (-∞;0]U[1,5;+∞)
Похожие вопросы
Предмет: Английский язык,
автор: araman94
Предмет: Алгебра,
автор: fomindaniil111
Предмет: Українська мова,
автор: Аноним
Предмет: Математика,
автор: Саприк