Question

20 баллов!!!!!!

сформулируйте и докажите теорему об окружности , описанной около правильного многоугольника

Answer 1

Около правильного многоугольника можно описать единственную окружность.

Доказательство:

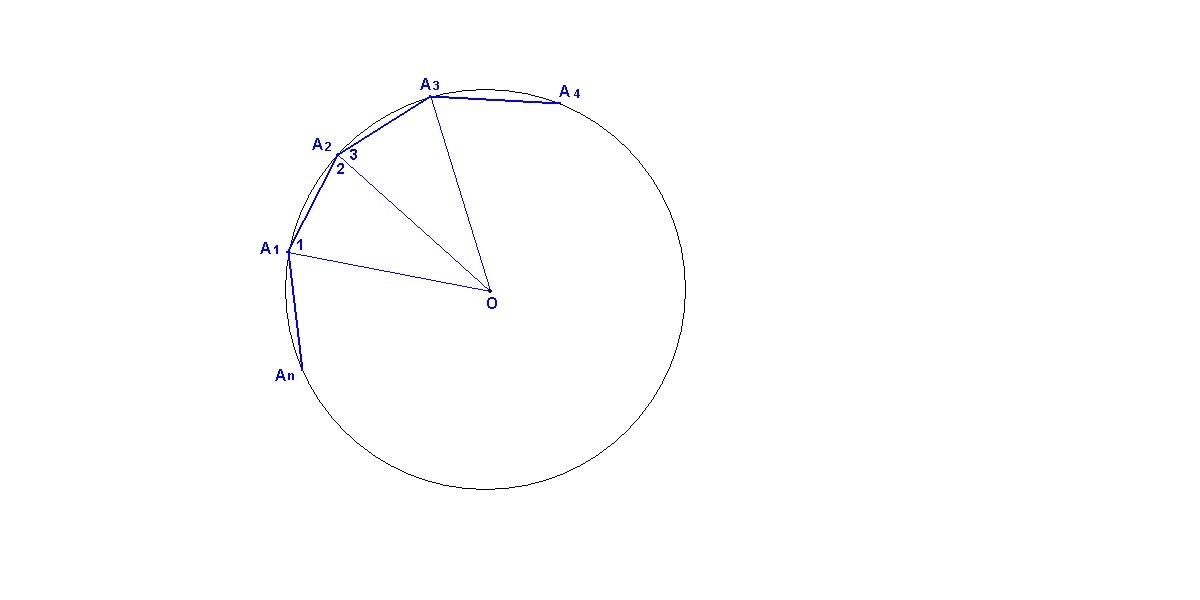
А₁А₂А₃... - правильный многоугольник.

Пусть биссектрисы углов А₁ и А₂ пересекаются в точке О.

Так как углы А₁ и А₂ многоугольника равны, то равны и углы 1 и 2.

Тогда ΔА₁ОА₂ - равнобедренный, т.е. точка О равноудалена от вершин А₁ и А₂.

∠3 = ∠2, так как ОА₂ биссектриса, центральные углы правильного многоугольника равны (∠А₁ОА₂ = ∠А₂ОА₃), сторона ОА₂ общая для треугольников А₁ОА₂ и А₂ОА₃, значит треугольники равны по стороне и двум прилежащим к ней углам.

Тогда ОА₃ = ОА₁.

Аналогично можно доказать, что равны и остальные треугольники. Таким образом, точка О равноудалена от всех вершин, значит она - центр описанной окружности.

Эта окружность будет описана и около треугольника, например, А₁А₂А₃, а вокруг треугольника можно описать единственную окружность, значит данная окружность - единственная, которую можно описать около правильного многоугольника.