Предмет: Геометрия,
автор: aider1995
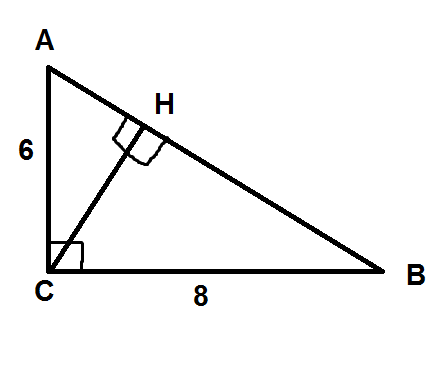
отрезок CH - высота треугольника ABC , в котором угол C = 90 градусов AC = 6 см и BC = 8 см найдите AB AH и HB
Ответы
Автор ответа:
0
по теореме пифагора найдем АВ:
АВ=√АС^2+CB^2=√36+64=√10=10 см
площадь прямоуг. треуг. = 1/2*а*, где a и b - катеты
площадь треуг.= 1/2*а*h, где a - сторона, на которую опирается h
получается, что 1/2*а*b = 1/2*а*h
1/2*6*8=1/2*10*h
24=5h
h=24:5=4,8 см - НС
в треуг. СНВ угол СНВ - прямой
по теореме пифагора найдем НВ:
НВ=√ 8^2 - 4,8^2 = √40,96 = 6,4 см
АН=АВ-НВ=10-6,4=3,6 см
АВ=√АС^2+CB^2=√36+64=√10=10 см
площадь прямоуг. треуг. = 1/2*а*, где a и b - катеты
площадь треуг.= 1/2*а*h, где a - сторона, на которую опирается h
получается, что 1/2*а*b = 1/2*а*h
1/2*6*8=1/2*10*h
24=5h
h=24:5=4,8 см - НС
в треуг. СНВ угол СНВ - прямой
по теореме пифагора найдем НВ:
НВ=√ 8^2 - 4,8^2 = √40,96 = 6,4 см
АН=АВ-НВ=10-6,4=3,6 см
Приложения:
Похожие вопросы
Предмет: Математика,
автор: aiko2409
Предмет: Математика,
автор: a22591
Предмет: Физика,
автор: mazhaevad
Предмет: Физика,
автор: logical
Предмет: Физика,
автор: Алексия911