Question

Помогите пожалуйста, может кто решал, только не из интернета.
Задача 1:
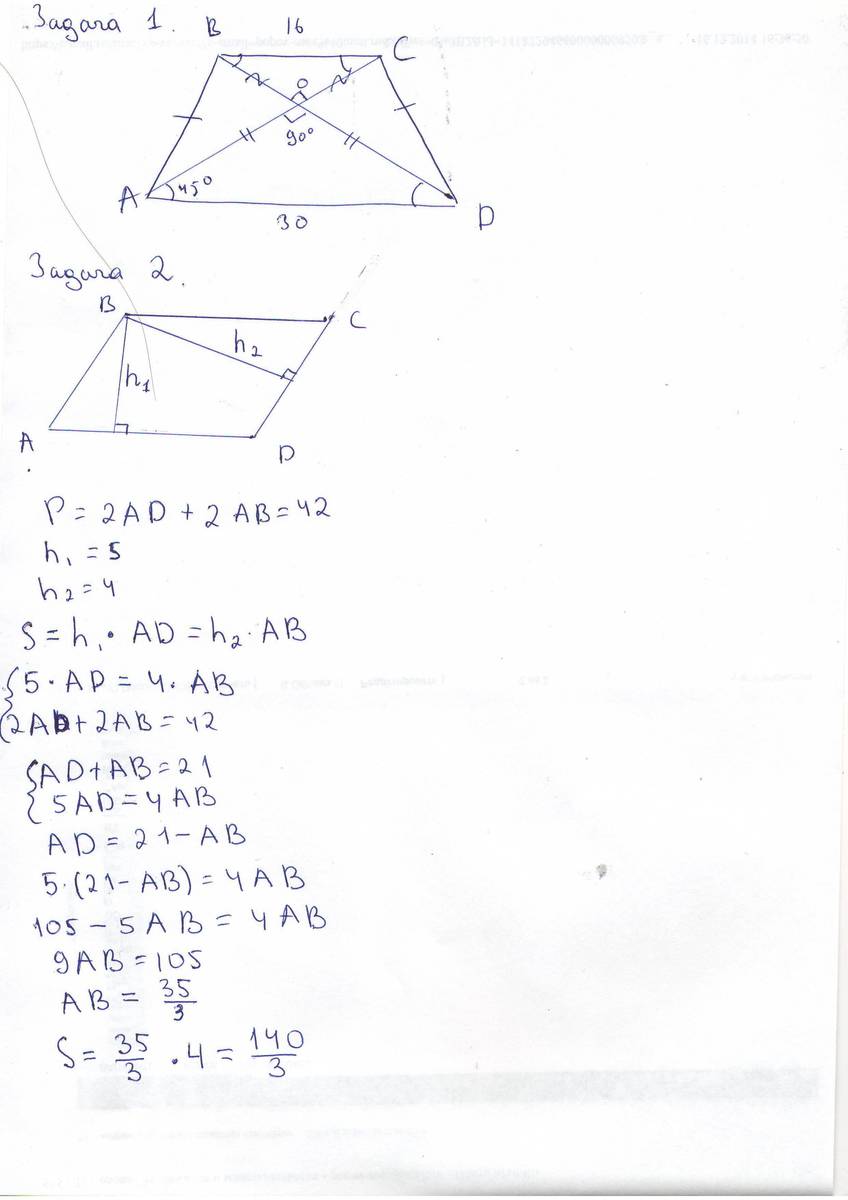
Найдите площадь равнобедренной трапеции если: ее основания равны 16 см и 30 см, а диагонали взаимно перпендикулярны.
Задача 2:
Высоты параллелограмма равны 5 см и 4см, а периметр равен 42 см. Найдите площадь параллелограмма.

Answer 1

Пусть трапеция ABCD, BC и AD основания равнобедренной  трапеции, O т. пересечения диагоналей.
Для начала рассмотрим треугольник AOD , т.к. трапеция ранобедренная, то углы CAD=BDA, а значит CAD=BDA=(180-90)/2=45°
AO²+OD²=30²
2AO²=900
AO²=450
AO=15√2
Рассмотрим треугольник BCO.
Т.к. трапеция равнобедренная, то углы CBD=CAD=(180-90)/2=45°
OB²+OC²=16²
2OC²=256
OC²=128
OC=8√2
Значит диагонали BD=AC=AO+OC=8√2+15√2=23√2
Формула площади трапеции через диагонали:
S=1/2*AC*BD*sin90=1/2*23√2*23√2*1=23²=529

Answer 2

Спасибо большое. насчет второго не знаешь?

Answer 3

Сейчас скан добавлю

Answer 4

это 2 задача?

Answer 5

Там где написано ЗАДАЧА2, ВВЕРХУ РИСУНОК К ЗАДАЧЕ1