Question

Сделайте пожалуйста номер 26
Напишите решение и рисунок.
Ответ будет (54+-4 корень из 26)/25
Кто первый сделает поставлю ЛУЧШИЙ
заранее спасибо

Answer 1

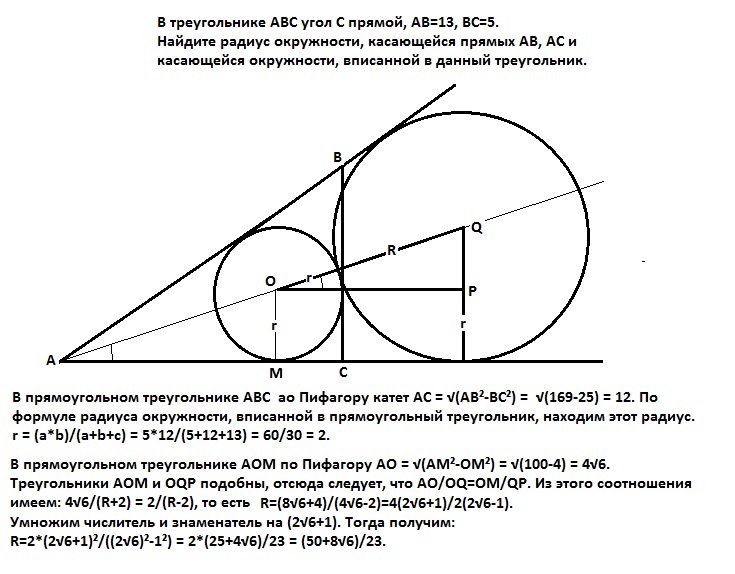
В прямоугольном треугольнике АВС по Пифагору катет АС = √(АВ²-ВС²) = √(169-25) = 12.
По формуле радиуса окружности, вписанной в прямоугольный треугольник, находим этот радиус.
Он равен r= a*b/(a+b+c), где a и и - катеты, а с - гипотенуза. У нас r= 5*12/(5+12+13) = 60/30 = 2.
В прямоугольном треугольнике АОМ по Пифагору АО = √(АМ²-ОМ²) = √(100-4) = 4√6.
Треугольники АОМ и OQP подобны, отсюда следует, что АО/OQ=ОМ/QP. Из этого соотношения имеем: 4√6/(R+2) = 2/(R-2), то есть R=(8√6+4)/(4√6-2)=4(2√6+1)/2(2√6-1).
Умножим числитель и знаменатель на (2√6+1). Тогда получим:
R=2*(2√6+1)²/((2√6)²-1²) = 2*(25+4√6)/23 = (50+8√6)/23.

Answer 2

Верно. В архив.