Question

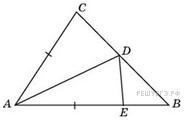
. В треугольнике ABC угол B равен 50, угол C равен 55 , AD — биссектриса, E — такая точка на AB, что АЕ=АС . Найдите угол BDE. Ответ дайте в градусах.

Answer 1

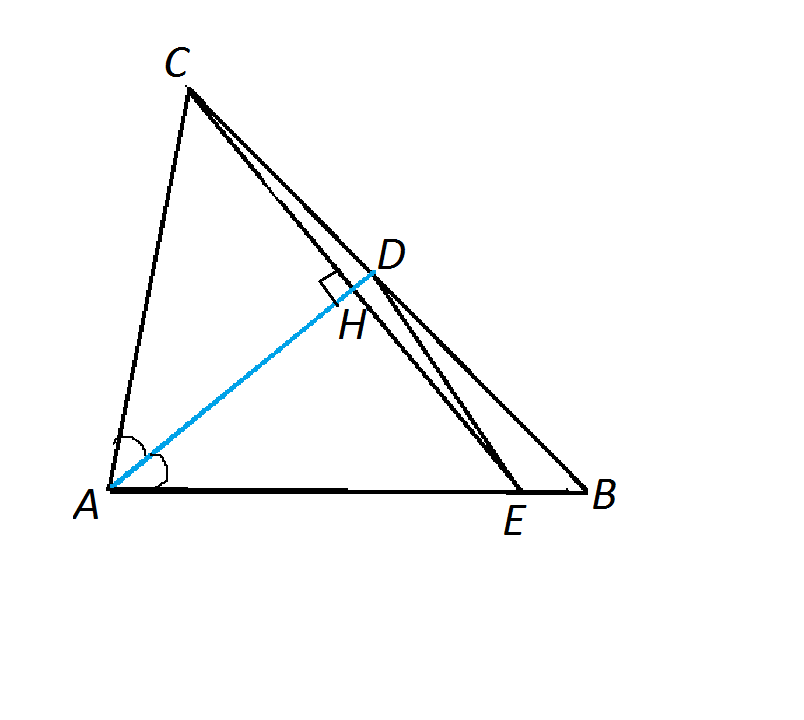
Угол САВ равен 180°-(50°+55°)=75°
Соединим С и Е.
Углы при основании СЕ равны, т.к. АС=АЕ и Δ АСЕ равнобедренный. 
∠АСЕ=∠АЕС=(180°-75°):2=52,5°
Треугольник АСЕ - равнобедренный, АD в нем биссектриса, следовательно, она же высота и медиана этого треугольника.
Обозначим точку пересечения АD и СЕ буквой Н. 
СН=ЕН, т.к. АН - медиана треугольника АСЕ. Но она же медиана и высота треугольника СDE.
Следовательно, треугольник СDЕ - равнобедренный.
В нем углы при основании СЕ равны углу ЕСВ, т.е.
∠ЕСВ=∠АСВ-∠АСЕ=55°-52,5°=2,5°
∠ЕСD=∠DEC=2,5°
Угол при вершине D треугольника АDE  равен 180°-2*2,5°=175°
Искомый ∠ ВDЕ=180°-175°=5°