Предмет: Геометрия,
автор: kristina100498
Основание пирамиды - квадрат с периметром 16 см. Две смежные боковые грани пирамиды перпендикулярны плоскости основания.Площадь меньшего диагонального сечения пирамиды вдвое меньше площади основания. Найдите площадь большего диагонального сечения.
Ответы
Автор ответа:
0
Р(осн)=4а
4а=16
а=4
Сторона основания равна 4 см
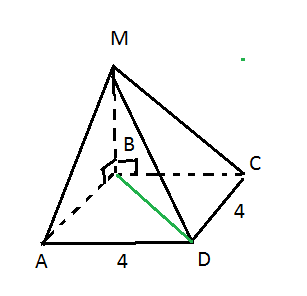
Меньшее диагональное сечение - Это сечение МВD. Так как это прямогольный треугольник.
По условию его площадь равна половине площади основания
S(осн)=4·4=16 кв. см
S(ΔMBD)=8 кв см
Диагонали квадрата равны
ВD=√(4²+4²) = 4√2 cм = АС
S(ΔMBD)=MB·BD/2
MB=2S:BD=16:4√2=2√2 см
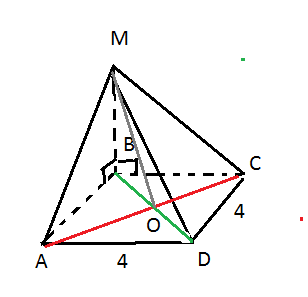
Найдем высоту МО второго диагонального сечения.
О- точка пересечения диагоналей
Из треугольника МВО
МО²=МВ²+ВО²=(2√2)²+(2√2)²=8+8=16
МО=4 см
S(ΔMAC)=AC·MO/2=4√2·4/2=8√2 кв. см
4а=16
а=4
Сторона основания равна 4 см
Меньшее диагональное сечение - Это сечение МВD. Так как это прямогольный треугольник.
По условию его площадь равна половине площади основания
S(осн)=4·4=16 кв. см
S(ΔMBD)=8 кв см
Диагонали квадрата равны
ВD=√(4²+4²) = 4√2 cм = АС
S(ΔMBD)=MB·BD/2
MB=2S:BD=16:4√2=2√2 см
Найдем высоту МО второго диагонального сечения.
О- точка пересечения диагоналей
Из треугольника МВО
МО²=МВ²+ВО²=(2√2)²+(2√2)²=8+8=16
МО=4 см
S(ΔMAC)=AC·MO/2=4√2·4/2=8√2 кв. см
Приложения:
Автор ответа:
0
Верно. В архив.
Похожие вопросы
Предмет: Литература,
автор: kincelapola
Предмет: Геометрия,
автор: hamuthab123
Предмет: Алгебра,
автор: polinka20070802
Предмет: Химия,
автор: Fromas12
Предмет: Обществознание,
автор: vihrova2801