Предмет: Алгебра,
автор: ishukdiana
решить системы ур-ний: 1) х^2=3х+4у, у^2=4х+3у
2)х^2-4x+4y+27=0, y^2+2x+8y+10=0
Ответы
Автор ответа:
0
Не уточнено каким методом решать,так что берем самый "простой" -графический.
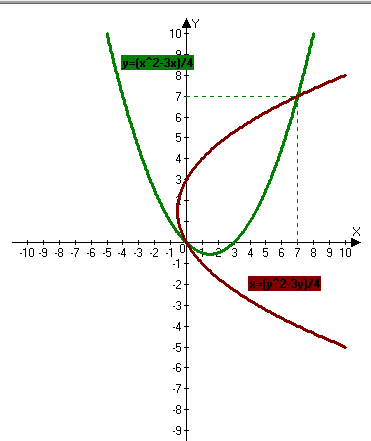
a)Для начала преобразуем уравнения системы:

Теперь строим каждое из уравнений(самое простое:по точкам,готовый вариант во вложении) и находим координаты точек пересечения,они и будут решениями.
В данном случае решениями системы будут точки (0;0) и (7;7)
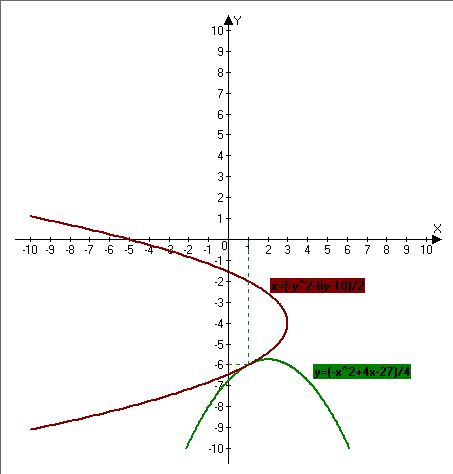
б)Та же схема,напишу только преобразования:

Решение системы здесь только одно:(1;-6)
a)Для начала преобразуем уравнения системы:
Теперь строим каждое из уравнений(самое простое:по точкам,готовый вариант во вложении) и находим координаты точек пересечения,они и будут решениями.
В данном случае решениями системы будут точки (0;0) и (7;7)
б)Та же схема,напишу только преобразования:
Решение системы здесь только одно:(1;-6)
Приложения:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: Аноним
Предмет: Русский язык,
автор: Аноним
Предмет: Английский язык,
автор: alishaulabay75322
Предмет: Физика,
автор: макс696