Question

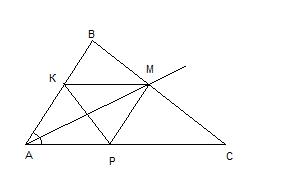
В треугольнике ABC проведена биссектриса AM. Отрезок MK параллелен стороне AC и пересекает AB в точке K, MP параллельна AB и пересекает AC в точке P. Докажите, что прямые AM и KP перпендикулярны.

Answer 1

Рассмотрим четырехугольник АКМР. Это параллелограмм, т.к. его противоположные стороны попарно параллельны по условию (KM II AP, AK II PM).
<KMA=<PAM как накрест лежащие углы при пересечении двух параллельных прямых АР и КМ секущей АМ. Но 
<PAM=<KAM по условию (АМ - биссектриса), значит
<KMA=<KAM, и треугольник АКМ - равнобедренный (углы при его основании АМ равны между собой). Значит
АК=КМ, а поскольку в параллелограмме противоположные стороны равны, то
АК=КМ=РМ=АР, и АКМР - ромб. 
Зная свойство диагоналей ромба (диагонали ромба взаимно перпендикулярны), делаем вывод, что КР перпендикулярна АМ.