Question

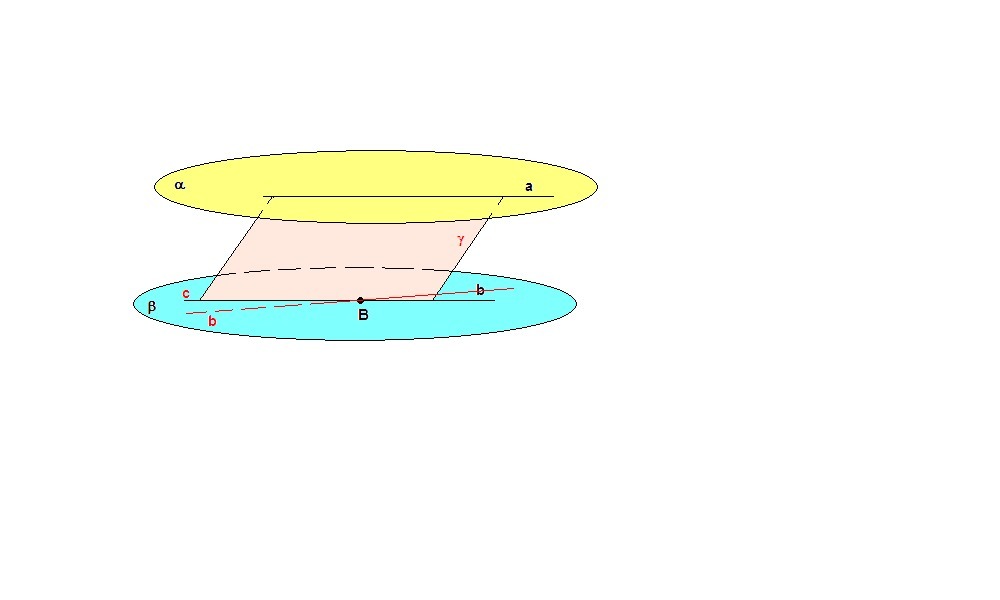
плоскости альфа и бета параллельны. Прямая а лежит в плоскости а. Через точку В, лежащую в плоскости бета, проведена  прямая b, параллельная a   Докажите, что b лежит   в плоскости бета

Answer 1

Прямая а параллельна прямой b. Через две параллельные прямые можно провести единственную плоскость. Проведем плоскость γ через прямые а и b.

Эта плоскость пересекает параллельные плоскости α и β по параллельным прямым.

Предположим, что прямая b не лежит в плоскости β. Тогда плоскость γ пересекает плоскость α по прямой а (так как прямая а лежит в обеих плоскостях), а плоскость β по прямой с. Тогда с║а.

Так как точка В лежит на прямой b, то эта точка лежит и в плоскости γ и в плоскости β. Получается, что через точку В проведены две прямые, параллельные прямой а, а это невозможно. Значит прямая b лежит в плоскости β.