Question

Решите неравенство:
Корень 4-ой степени из x + 1  > 30/x

Answer 1

ОДЗ:

{х+1 ≥0⇒х≥-1

{x≠0

При $frac{30}{x}<0$  неравенство верно при любом х из ОДЗ

x∈[-1;0) - решение неравенства

При  $frac{30}{x}>0$ , т.е при x>0 возводим обе части неравенства в четвертую степень:

$x+1 > (frac{30}{x})^4$

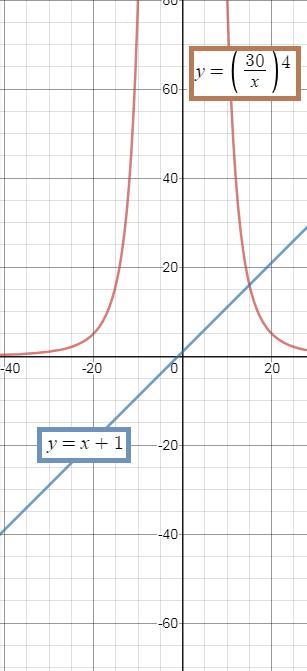
Решаем  неравенство графически:

См. рис.

Строим графики y=$(frac{30}{x})^4$ ( красного цвета)

$y`=-frac{4cdot30^4}{x^5} <0$

при x >0

кривая убывает.

Строим y=x+1 это прямая синего цвета, возрастает на (-∞;+∞)

Кривая и прямая пересекаются в одной точке, это х=15

Поэтому неравенство верно  при x > 15

О т в е т. [-1;0) U (15;+∞)

Answer 2

Ответ и Объяснение:

в приложении