Предмет: Геометрия,
автор: sofiasergo
Решите прошууууууу
В параллелограмме АВСД проведена биссектриса угла ВАД, которая пересекает ВС в точке Е.
1) Докажите, что треугольник АВЕ - равнобедренный
2) Найдите АД, если ВЕ-12 см, а Р параллелограмма (периметр параллелограмма)-48 см
Ответы
Автор ответа:
0
Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник.
Действительно, угол ВЕА треугольника АВЕ равен углу ЕАД как внутренние накрестлежащие углы при параллельных прямых ВС и АД и секущей АЕ.
Но по условию угол ВАЕ равен ЕАД, т.к. АЕ - биссектриса.
Следовательно, углы треугольника при основании АЕ равны, и треугольник АВЕ - равнобедренный, что и требовалось доказать.
--------
ВЕ по условию равна 12, следовательно, АВ также равна 12.
В параллелограмме противоположные стороны равны.
СД=АВ=12.
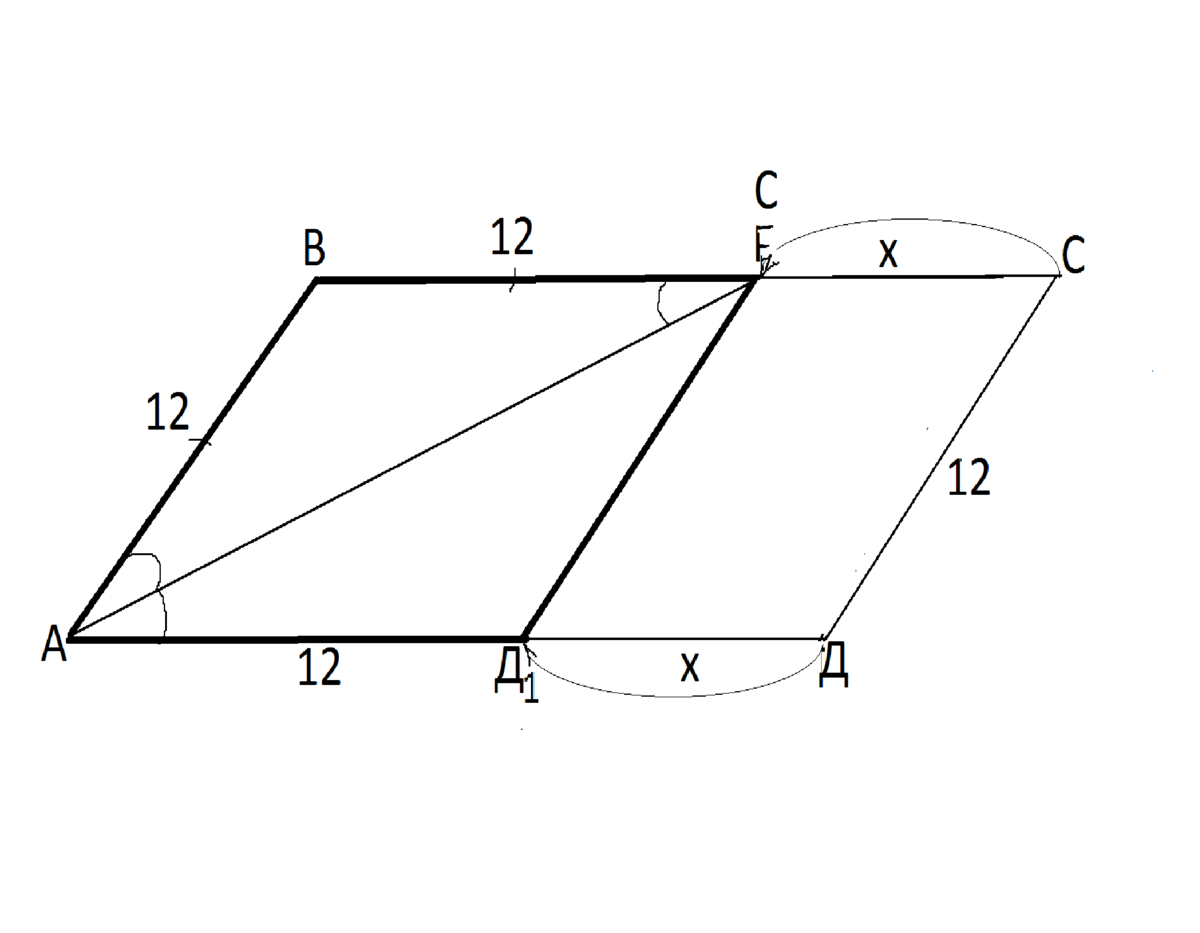
Проведем из Е параллельно АВ прямую ЕД1
АВЕД1 - параллелограмм по построению.
ЕД1=АВ.
ВЕ=АД1
Следовательно, АД1=12.
ЕСДД1 - параллелограмм по построению.
ЕС=ДД1 как стороны параллелограмма Д1ЕСД
Пусть ЕС и ДД1=х
Р (АВСД)=48
Р=12*4+2х=48
48+2х=48
2х=48-48=0
х=0
Отсюда следует, что Е совпадает с вершиной С, а Д1 совпадает с вершиной Д параллелограмма, АД=12, и этот параллелограмм - ромб.
Действительно, угол ВЕА треугольника АВЕ равен углу ЕАД как внутренние накрестлежащие углы при параллельных прямых ВС и АД и секущей АЕ.
Но по условию угол ВАЕ равен ЕАД, т.к. АЕ - биссектриса.
Следовательно, углы треугольника при основании АЕ равны, и треугольник АВЕ - равнобедренный, что и требовалось доказать.
--------
ВЕ по условию равна 12, следовательно, АВ также равна 12.
В параллелограмме противоположные стороны равны.
СД=АВ=12.
Проведем из Е параллельно АВ прямую ЕД1
АВЕД1 - параллелограмм по построению.
ЕД1=АВ.
ВЕ=АД1
Следовательно, АД1=12.
ЕСДД1 - параллелограмм по построению.
ЕС=ДД1 как стороны параллелограмма Д1ЕСД
Пусть ЕС и ДД1=х
Р (АВСД)=48
Р=12*4+2х=48
48+2х=48
2х=48-48=0
х=0
Отсюда следует, что Е совпадает с вершиной С, а Д1 совпадает с вершиной Д параллелограмма, АД=12, и этот параллелограмм - ромб.
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: azharlevina
Предмет: Математика,
автор: LyakBoy
Предмет: Физика,
автор: lomaki2007
Предмет: Химия,
автор: VredinaTata
Предмет: Математика,
автор: nastyakt