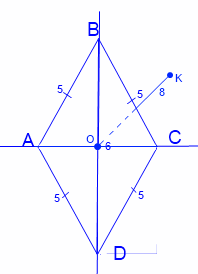
Длина стороны ромба ABCD равна 5 см, длина диагонали BD равна 6 см. Через точку O пересечения диагоналий ромба проведена прямая OK, перпендикулярная его плоскости. Найдите расстояние от точки К до вершин ромба, если ОК = 8см.
Ответы
Итак найдем:
найдем OB. Так как вся диагональ BD равна 6 см, то
OB = половине диагонали(в ромбе диагонали делят друг друга пополам) = 3
OB = 3
Рассмотрим теперь треугольник COB.
Данный треугольник прямоугольный (диагонали ромба перпендикулярны), значит
OC^2 = BC^2-OB^2
OC^2 = 5^2 - 3^2
OC^2 = 25-9
OC^2 = 16, значит OC = 4
Т.к. OK перпендикулярна плоскости ромба, то по теореме пифагора найдем расстояния:
Рассмотрим треугольник KOC
KO = 8 (по усл)
OC = 4 (нашли)
это катеты, значит
CK^2 = KO^2 + OC^2
CK^2 = 64 + 16 = 80
CK = примерно 8.94 см
Очевидно, что AK = CK = примерно 8.94 см
Найдем BK
BK^2 = 3^2 + 8^2
BK^2 = 9 + 64
BK^2 = 73
BK = примерно 8.54 см
Очевидно, что DK = BK = примерно 8.54 см
Ответ: Расстояния от K до вершин ромба следующие:
DK = BK = примерно 8.54 см
AK = CK = примерно 8.94 см
P.S. если равенство AK = CK не очевидно, то можно подставить значения в формулу длины - подставятся те же самые значения.
Задавайте вопросы