Предмет: Математика,
автор: nikitaaz
Исследовать на условную и абсолютную сходимость
Приложения:
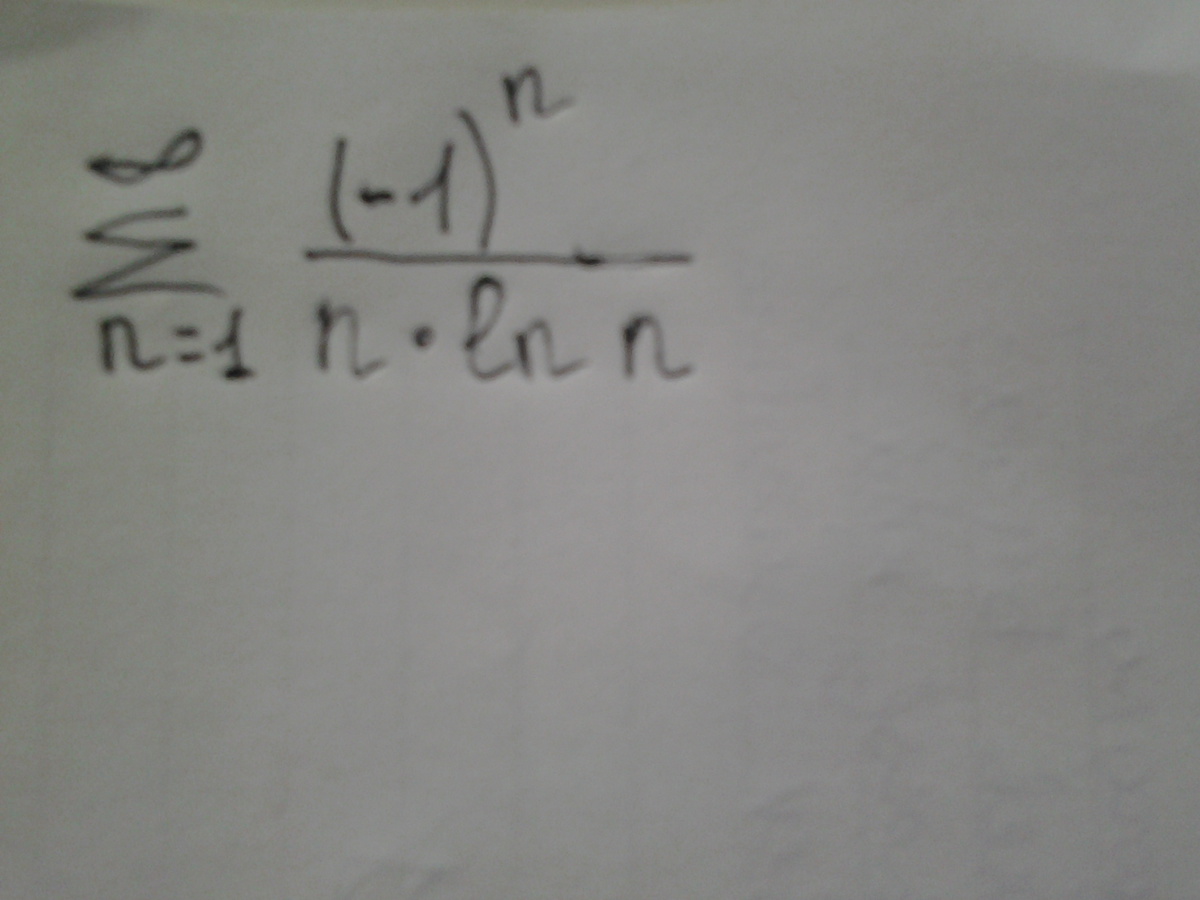
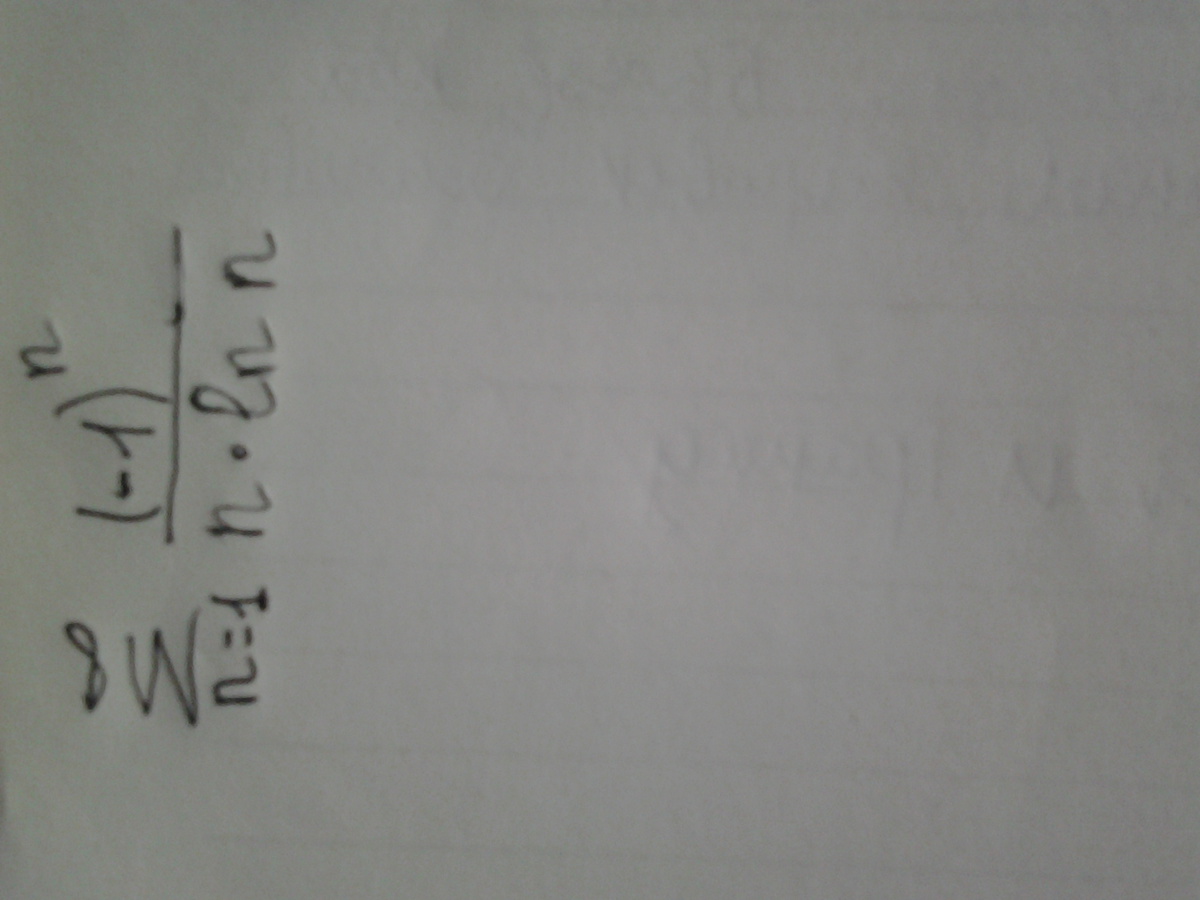
Ответы
Автор ответа:
0
Знакочередующийся ряд.
Только при n=1 ln1=0, а на ноль делить нельзя.
При п=1 до +∞ ряд не существует.
Значит, n≥2
Исследуем на сходимость по признаку Лейбница

Проверяем выполнение этих условий у данного ряда
верно, так как
(n+1)>n
ln(n+1)>lnn, для n>1
Перемножаем
(n+1)ln(n+1)>n·ln(n), n∈N
Знакопеременный ряд сходится по признаку Лейбница
К исследованию знакоположительного ряда
применяем интегральный признак

Несобственный интеграл расходится, значит и ряд расходится.
Ответ. Ряд сходится условно
Только при n=1 ln1=0, а на ноль делить нельзя.
При п=1 до +∞ ряд не существует.
Значит, n≥2
Исследуем на сходимость по признаку Лейбница
Проверяем выполнение этих условий у данного ряда
верно, так как
(n+1)>n
ln(n+1)>lnn, для n>1
Перемножаем
(n+1)ln(n+1)>n·ln(n), n∈N
Знакопеременный ряд сходится по признаку Лейбница
К исследованию знакоположительного ряда
применяем интегральный признак
Несобственный интеграл расходится, значит и ряд расходится.
Ответ. Ряд сходится условно
Похожие вопросы
Предмет: Английский язык,
автор: 59182eva
Предмет: Математика,
автор: mubtolla
Предмет: Информатика,
автор: gulsurehaciyeva97
Предмет: Физика,
автор: вит91735
Предмет: Алгебра,
автор: lena852