Предмет: Алгебра,
автор: petechka
решите симметрическую систему уранений
Приложения:
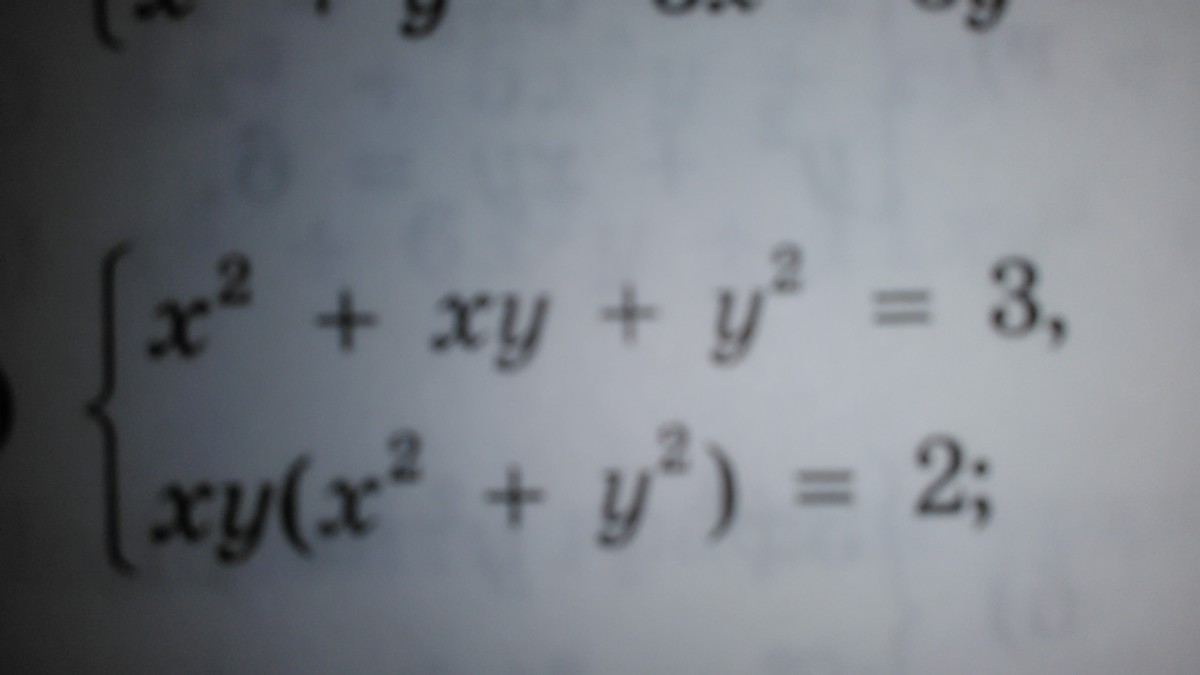
Ответы
Автор ответа:
0
x²+xy+y²=3
xy(x²+y²)=2
x²+xy+y²-3=0
x³y+xy³-2=0
Пусть x+y = u, xy = v
u²-v-3=0
u²v-2v²-2=0
u²-v-3=0
(u²-v-3)-(u²v-2v²-2)=0
-Проработаем со вторым уравнением
u²(1-v)+(-v-1+2v²)=0
-u²(-1+v)+(-1+v)(2v+1)=0
(-1+v)(-u²+2v+1)=0
Имеем что
u²-v-3=0
(-1+v)(-u²+2v+1)=0
Имеем 2 системы
u²-v-3=0 также u²-v-3=0
-1+v=0 -u²+2v+1=0
v=1 u²-v-3=0
u= v-2=0
v-2=0
v=2
u=
Обратная замена:
I Система
x+y=-2
xy=1
x=-2-y
(-2-y)y=1
y²+2y+1=0
(y+1)²=0
y=-1
x=-1 - Первая пара решение системы (-1;-1)
II система
x+y=2
xy=1
x=2-y
(2-y)y=1
y²-2y+1=0
(y-1)²=0
y=1
x=1 - Вторая пара решение системы (1;1)
III cистема
x+y=-√5
xy=2
x=-√5 - y
(-√5-y)y=2
y²+√5y+2=0
D=b² -4ac = -3 < 0. Нет решений.
Ответ: (-1;-1), (1;1)
xy(x²+y²)=2
x²+xy+y²-3=0
x³y+xy³-2=0
Пусть x+y = u, xy = v
u²-v-3=0
u²v-2v²-2=0
u²-v-3=0
(u²-v-3)-(u²v-2v²-2)=0
-Проработаем со вторым уравнением
u²(1-v)+(-v-1+2v²)=0
-u²(-1+v)+(-1+v)(2v+1)=0
(-1+v)(-u²+2v+1)=0
Имеем что
u²-v-3=0
(-1+v)(-u²+2v+1)=0
Имеем 2 системы
u²-v-3=0 также u²-v-3=0
-1+v=0 -u²+2v+1=0
v=1 u²-v-3=0
u=
v=2
u=
Обратная замена:
I Система
x+y=-2
xy=1
x=-2-y
(-2-y)y=1
y²+2y+1=0
(y+1)²=0
y=-1
x=-1 - Первая пара решение системы (-1;-1)
II система
x+y=2
xy=1
x=2-y
(2-y)y=1
y²-2y+1=0
(y-1)²=0
y=1
x=1 - Вторая пара решение системы (1;1)
III cистема
x+y=-√5
xy=2
x=-√5 - y
(-√5-y)y=2
y²+√5y+2=0
D=b² -4ac = -3 < 0. Нет решений.
Ответ: (-1;-1), (1;1)
Автор ответа:
0
Решаем второе уравнение относительно xy
xy(3-xy)=2
-(xy)²+3(xy)-2=0
или
(xy)²-3(xy)+2=0
квадратное уравнение
D=9-8=1
(xy)=(3-1)/2=1 или ху=(3+1)/2=2
тогда
х²+у²=3-1=2 или х²+у³=3-2=1
Решаем две системы.
умножили первое уравнение на (2) и
сложим уравнения, получим формулу квадрата суммы (х+у)²=4 ⇒х+у=2 или х+у = -2
при этом ху=1
Снова две системы
Решаем второе уравнение
2x-x²=1⇒x²-2x+1=0 ⇒ (x-1)²=0 ⇒ x₁=1 тогда у₁=2-1=1
Решаем второе уравнение
-2x-x²=1⇒x²+2x+1=0 ⇒ (x+1)²=0 ⇒ x₂=-1 тогда у₂=-2-(-1)=-1
умножили первое уравнение на (2) и
сложим уравнения, получим формулу квадрата суммы (х+у)²=5 ⇒х+у=√5 или х+у = -√5
при этом ху=2
Снова две системы
Решаем второе уравнение
√5x-x²=2⇒x²-√5·x+2=0
D=(√5)²-4·2<0 уравнение не имеет решений
Значит эта система не имеет решений
Решаем второе уравнение
-√5·x-x²=2⇒x²+√5x+1=0
D=(√5)²-4·2<0 уравнение не имеет решений
Значит и эта система не имеет решений
Ответ. (1;1) (-1;-1)
Похожие вопросы
Предмет: Литература,
автор: oksana200845
Предмет: Математика,
автор: noidex
Предмет: Физика,
автор: ButterCuP15
Предмет: Литература,
автор: pahom12
Предмет: Алгебра,
автор: fkbyffkbyffkbyffkbyf