Предмет: Геометрия,
автор: vhlam
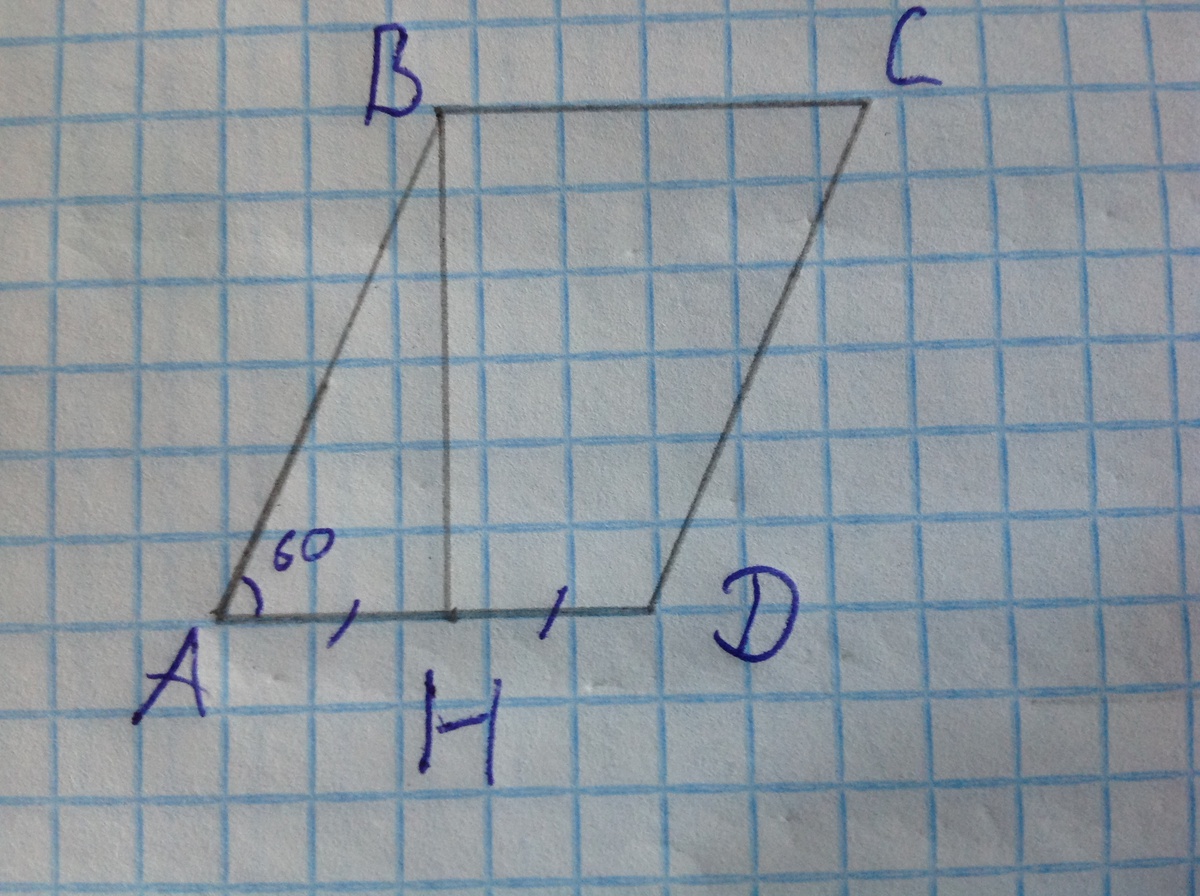
Даю 15 баллов. В параллелограмме острый угол равен 60 градусов. Высота параллелограмма, проведенная из вершины тупого угла, делит сторону параллелограммапополам. Найдите меньшую диагональ параллелограмма, если его периметр равен 24.
Ответы
Автор ответа:
0
Пусть в параллелограмме ABCD угол A равен 60 градусам, а высота BH делит сторону AD пополам (см. рисунок). Рассмотрим прямоугольный треугольник ABH. В нём острый угол HAB равен 60 градусам, тогда другой острый угол - ABH - равен 90-60=30 градусам. Известно, что в прямогольном треугольнике катет, лежащий против угла в 30 градусов, равен половине гипотенузы. Значит, AB=2AH. Кроме того, AD=2AH, значит, AB=AD. По свойству параллелограмма, AB=CD; AD=BC, это значит, что все стороны нашего параллелограмма равны между собой, тогда каждая из них равна 1/4 периметра. В частности, AB=AD=24/4=6. Теперь рассмотрим треугольник ABD. В него входит меньшая диагональ параллелограмма - BD. Нам известно, что этот треугольник равнобедренный, так как AB=AD. Так как угол при вершине равен 60 градусам, 2 других угла треугольника также равны 60 градусам. Значит, треугольник равносторонний и AB=AD=BD. Отсюда BD=6.
Приложения:
Похожие вопросы
Предмет: Математика,
автор: ruhernik9
Предмет: Українська література,
автор: anutavoznuk
Предмет: Физика,
автор: dinaraizmahunova79
Предмет: Химия,
автор: Alyonaponikarova
Предмет: Математика,
автор: Strahylka