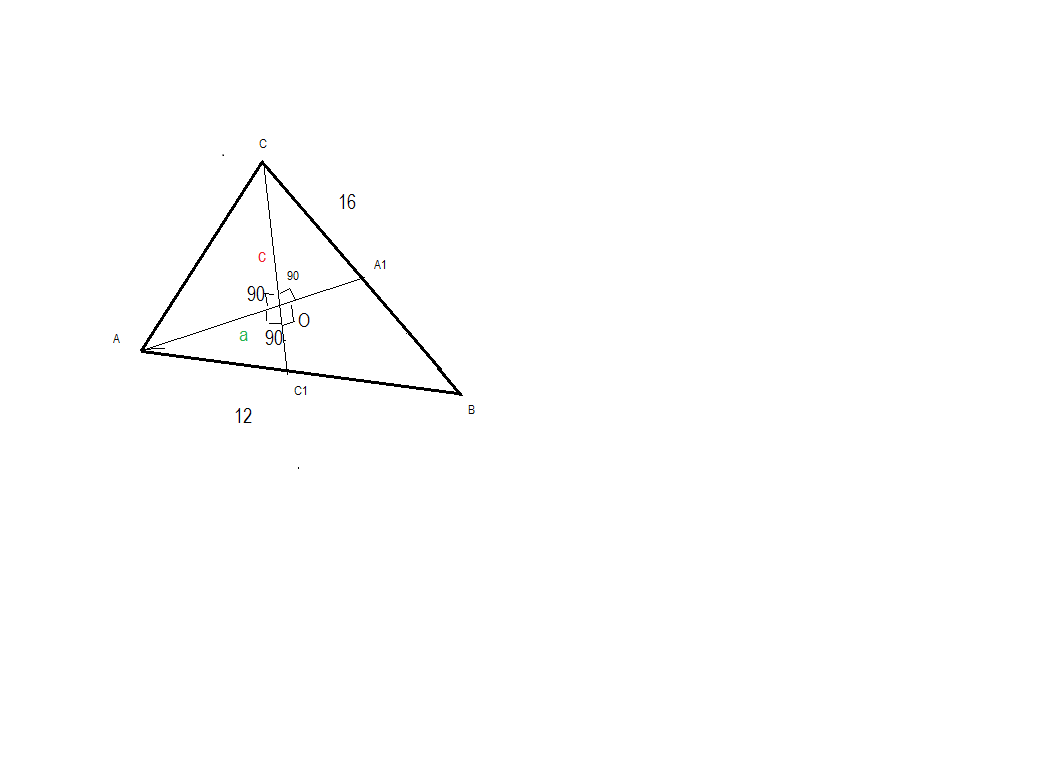
в треугольник АВС сторона АВ=12см ВС=16 медианы треугольника АА1 и СС1 пресекаются под углом 90 градусов найдите длинну стороны АС в ответе запишите АС корень из 5
Ответы
пусть
длина медаины АА1=а
длина медины СС1=с
точка персечения О делит медианы на отрезки -свойство медиан
СО=2/3*с
ОС1=1/3*с
АО=2/3*а
ОА1=1/3*а
треугольники АОС1 и СОА1 - прямоугольные ,
т к медианы треугольника АА1 и СС1 пресекаются под углом 90 градусов
тогда по теореме Пифагора
СО^2 +OA1^2 =CA1^2 подставим сюда а , c CA1=16/2
(2/3*с)^2 +(1/3*а)^2= (16/2)^2 (1)
ОC1^2 +OA^2 =AC1^2 подставим сюда а , c AC1=12/2
(1/3*с)^2 +(2/3*а)^2= (12/2)^2 (2)
решим систему двух уравнений (1) и (2)
здесь а =4√3 с=2√33
теперь найдем сторону АС
по теореме Пифагора
АС^2= (2/3*c)^2 +(2/3*a)^2=(2/3)^2*(c^2+a*2)=(2/3)^2*((2√33)^2+(4√3)^2)=80
AC=√80 =4√5
Ответ AC=4√5