Question

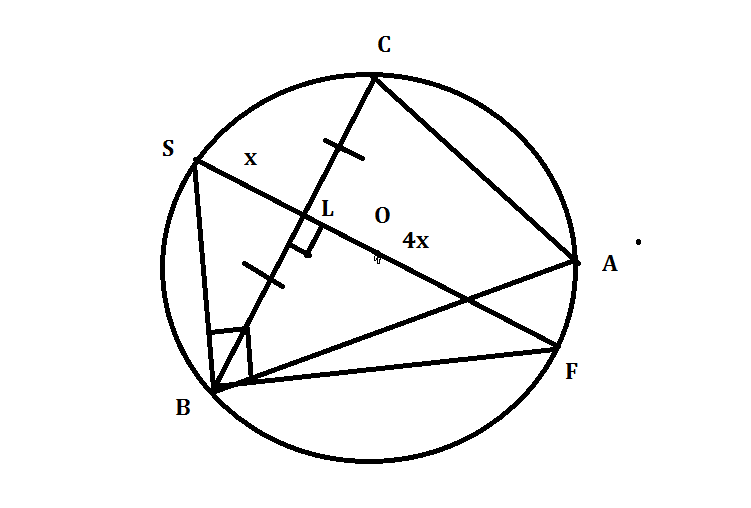
Около треугольника ABC со стороной AC=5 описана окружность с диаметром 5*sqrt(13)/2. Сторона BC делит диаметр окружности, перпендикулярный ей, на отрезки, длины которых относятся как 1:4. Найдите сторону AB треугольника.

Answer 1

диаметр делит BC  пополам тк перпендикулярен  хорде.
5x=5sqrt(13)/2
x=sqrt(13)/2
Треугольник SBF  прямоугольный. А  BL его высота.
Откуда по  теореме высоты  получим: BL=sqrt(4x^2)=2x=sqrt(13)
BC=2sqrt(13). a=AB
По  теореме синусов   5/sinB=2R=5sqrt(13)/2   sinB=2/sqrt(13)
cosB=sqrt(1-4/13)=3/sqrt(13)
По  теореме косинусов AB=a
a^2+52-2*3/sqrt(13) *a*2sqrt(13)=25
a^2+52-8a=25
a^2-12a+27=0
По  виету:
a=9
a=3
Ответ: AB=3 или 9 Выходит  2 возможных  ответа.