Question

ПОМОГИТЕ!  Несколько дней не могу решить, отчаялась уже!   До завтра времени осталось...
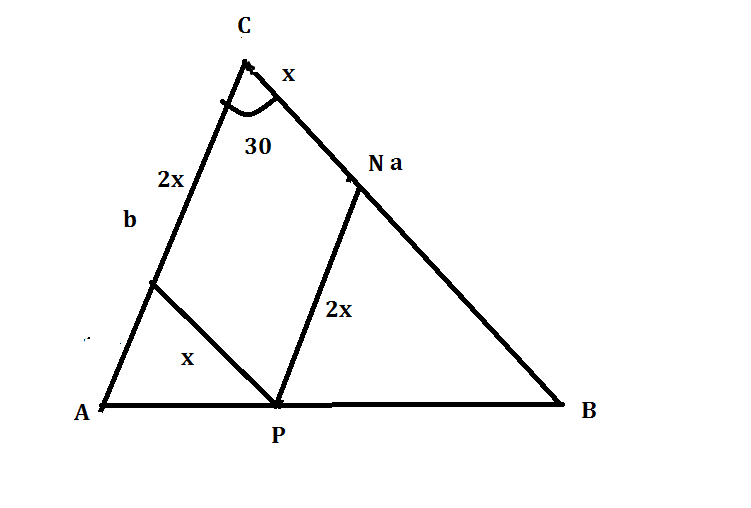
В треугольнике АВС BC = a, AC = b, угол ACB равен 30°. Найдите
площадь параллелограмма, имеющего с треугольником АВС общий угол С, если
вершина противоположного угла параллелограмма лежит на АВ, а одна
сторона параллелограмма вдвое больше другой.

Answer 1

Треугольники  ABC и PNB подобны по  соответственным углам.
b/2x=a/(a-x)
b(a-x)=2ax
ab-bx=2ax
ab=(2a+b)x
x=ab/(2a+b)
Площадь: S=x*2x*sin30=a^2b^2/(2a+b)^2