Предмет: Алгебра,
автор: JuliaLis991
При каких значениях K уравнение имеет единственный корень?
Приложения:
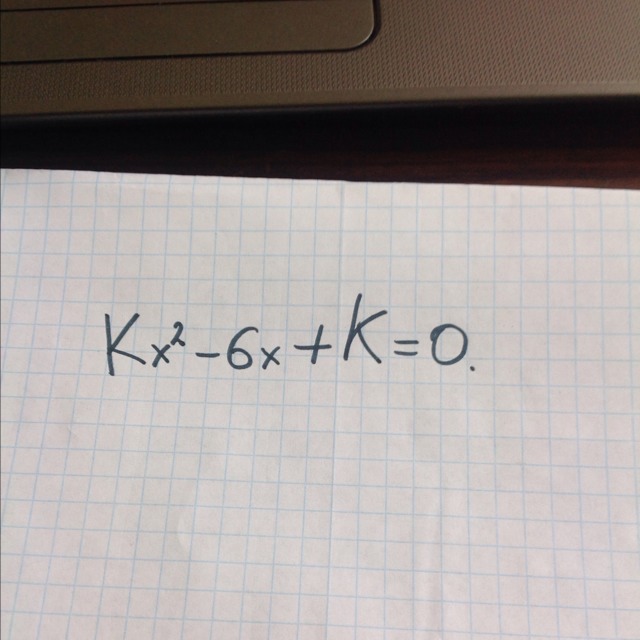
Ответы
Автор ответа:
0
Квадратное уравнение имеет единственный корень, если дискриминант этого уравнения равен 0
kx²-6x+k=0,
D=(-6)²-4k·k=36-4k²
36-4k²=0
4k²=36
k²=9
k=3 или k=-3
Ответ. k=3 или k=-3
kx²-6x+k=0,
D=(-6)²-4k·k=36-4k²
36-4k²=0
4k²=36
k²=9
k=3 или k=-3
Ответ. k=3 или k=-3
Автор ответа:
0
кх²-6х+к=0
Данное уравнение квадратное, оно имеет один корень, когда его дискриминант равен нулю.
Д=36-4*к*к=36-4к²
36-4к²=0 ⇔ -4к²=-36 ⇔ к²=9 ⇒ к=+-3.
При значениях к=+-3 уравнение имеет один корень.
Данное уравнение квадратное, оно имеет один корень, когда его дискриминант равен нулю.
Д=36-4*к*к=36-4к²
36-4к²=0 ⇔ -4к²=-36 ⇔ к²=9 ⇒ к=+-3.
При значениях к=+-3 уравнение имеет один корень.
Похожие вопросы
Предмет: Биология,
автор: wildfirewow7
Предмет: Физкультура и спорт,
автор: Аноним
Предмет: Қазақ тiлi,
автор: balnurzainelova10
Предмет: Физика,
автор: meower
Предмет: Математика,
автор: Jdg700