Question

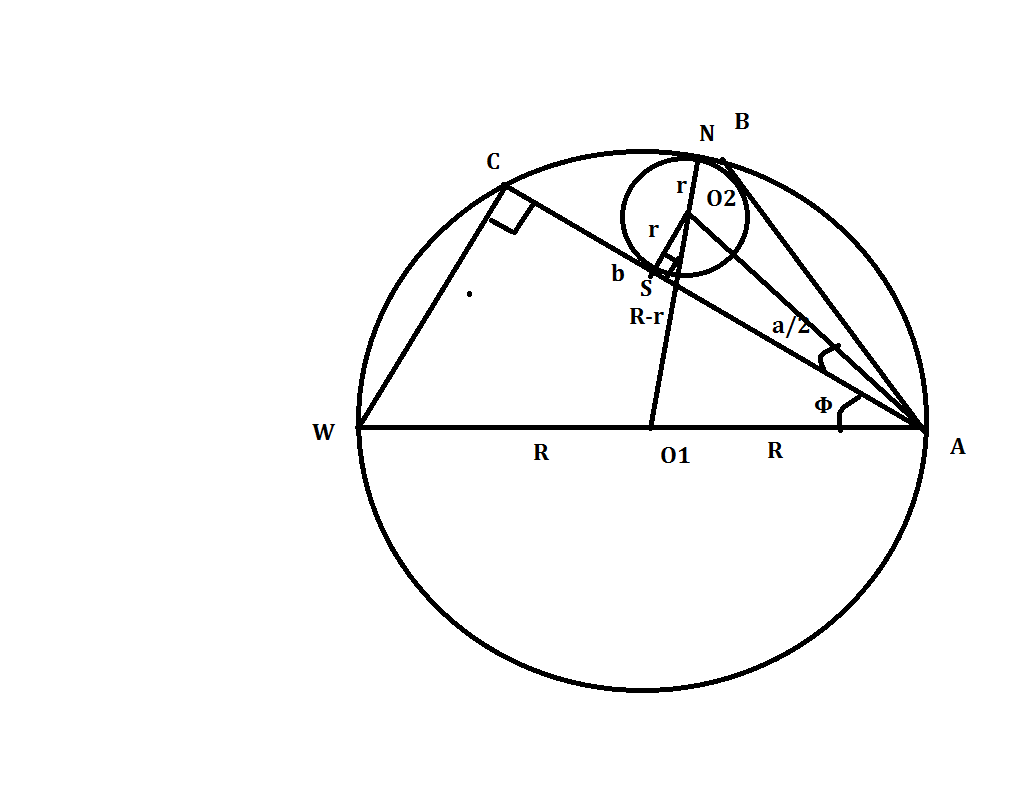
Из точки  A, лежащей на окружности радиуса  R проведены две хорды – AC  и AB.  Эти хорды лежат по одну сторону от диаметра окружности, проходящего через точку  A.  Дана длина b большей хорды и угол  BAC = a. Найти радиус окружности,которая касается хорд  AB и  AC и дуги  BC.

Answer 1

Пусть N точка касания малой окружности с дугой. ТО  по  теореме внутреннего касания окружностей. O1N=R
Причем  O1N  проходит через центр малой окружности,откуда
O1O2=R-r
Треугольник WCA-прямоугольный   тк опирается на диаметр,то
сosФ=b/2R
Тк   малая окружность   вписана в угол ABC,то  ее центр лежит  на бессектрисе этого угла (AO2)
Проведем из   центра  O2 радиус   к точке касания (радиус всегда  перпендикулярен   касательной)
Откуда AO2=r/sin(a/2)
угол  Ф=arccos(b/2R)
Запишем теорему косинусов  для треугольника AO1O2
R^2+r^2/sin^2(a/2)-2Rr*cos(a/2+arccos(b/2R))/sin(a/2)=(R-r)^2
Ну  давайте разбираться :)
(R-r)^2=R^2-2Rr+r^2
R^2  cокращается тогда можно  еще  поделить  на r
r/sin^2(a/2)-2R*cos(a/2+arccos(b/2R)/sin(a/2)=r-2R
r*ctg^2(a/2)=2R*(cos(a/2+arccos(b/2R))-sin(a/2))/sin(a/2)
r=2R*sin(a/2)*(cos(a/2+arccos(b/2R))-sin(a/2))/cos^2(a/2)
Вы  можите   конечно раскрыть косинус суммы может что хорошее получится. Но  боюсь  вы сойдете с ума :)
Желаю удачи. Помог как смог