Предмет: Математика,
автор: mstyutinnikova
Прошу кто знает ,помогите найдите наименьшее значение функции y=6tgx-12x+3pi-3 на отрезке [-pi/3; pi/3]
пожалуйста помогите
Ответы
Автор ответа:
0
y = 6*tg(x) - 12*x + 3*pi - 3
y ' = 6/cos^2(x) - 12
y ' = 0
6/cos^2(x) = 12
cos^2(x) = 6/12
cos^2(x) = 1/2
cos(x) = ±√2/2
x = pi/4 + pi*k/2 - критические точки
отрезку [-pi/3; pi/3] принадлежат критические точки х1=-pi/4; x2=pi/4
y (x=pi/4) = 6tg(pi/4) - 3pi + 3pi - 3 = 6 - 3 = 3
y (x=-pi/4) = -6tg(pi/4) + 3pi + 3pi - 3 = 6pi - 9 ~ 9,849556
y (x=-pi/3) = -6tg(pi/3) + 4pi + 3pi - 3 = 7pi - 3 - 6*корень(3) ~ 8,598844
y (x=pi/3) = 6tg(pi/3) - 4pi + 3pi - 3 = -pi - 3 + 6*корень(3) ~ 4,250712
минимальное значение достигается при y (x=pi/4)
ответ 3
********************
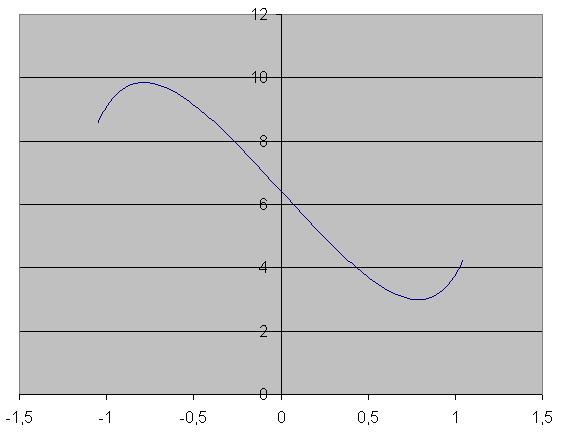
на рисунке 1 график функции y = 6*tg(x) - 12*x + 3*pi - 3 на отрезке [-pi/3; pi/3]
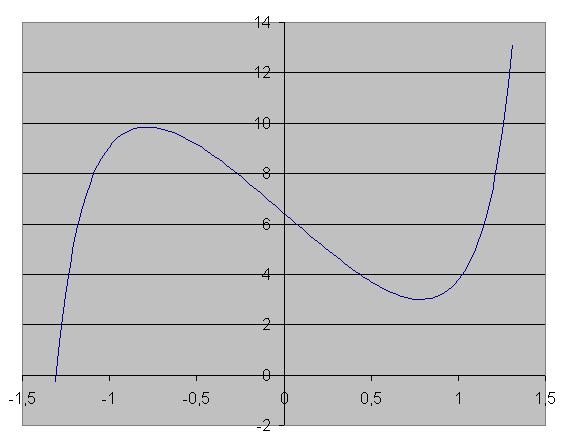
на рисунке 2 график функции y = 6*tg(x) - 12*x + 3*pi - 3 на отрезке [-5pi/12; 5pi/12]
(функция та-же, но диапазон чуть шире)
y ' = 6/cos^2(x) - 12
y ' = 0
6/cos^2(x) = 12
cos^2(x) = 6/12
cos^2(x) = 1/2
cos(x) = ±√2/2
x = pi/4 + pi*k/2 - критические точки
отрезку [-pi/3; pi/3] принадлежат критические точки х1=-pi/4; x2=pi/4
y (x=pi/4) = 6tg(pi/4) - 3pi + 3pi - 3 = 6 - 3 = 3
y (x=-pi/4) = -6tg(pi/4) + 3pi + 3pi - 3 = 6pi - 9 ~ 9,849556
y (x=-pi/3) = -6tg(pi/3) + 4pi + 3pi - 3 = 7pi - 3 - 6*корень(3) ~ 8,598844
y (x=pi/3) = 6tg(pi/3) - 4pi + 3pi - 3 = -pi - 3 + 6*корень(3) ~ 4,250712
минимальное значение достигается при y (x=pi/4)
ответ 3
********************
на рисунке 1 график функции y = 6*tg(x) - 12*x + 3*pi - 3 на отрезке [-pi/3; pi/3]
на рисунке 2 график функции y = 6*tg(x) - 12*x + 3*pi - 3 на отрезке [-5pi/12; 5pi/12]
(функция та-же, но диапазон чуть шире)
Приложения:
Похожие вопросы
Предмет: Литература,
автор: irairina287
Предмет: Биология,
автор: 7287710
Предмет: Геометрия,
автор: daler4ik16
Предмет: История,
автор: oksanarudenko1