Предмет: Математика,
автор: MatthewBerner
Решите уравнение с модулями.
||x+3|-|x-5||=8
Ответы
Автор ответа:
0
Решим отдельно
|x+3|-|x-5|=8
В систему
{x+3≥0
{x+3-|x-5|=8
{x≥-3
{x+3-|x-5|=8
{x≥-3
{x-5≥0
{x+3-(x-5)=8
{x≥-3 {x≥5
{x≥5 ⇒ {8=8 ⇒ x≥5
{x+3-x+5=8
----------------------------------
{x≥-3 { -3≤x<5
{x-5<0 ⇒ {x=5 Подставим в неравенство 5 и
{x+3+x-5=8 получаем что решений не имеет
Ответ уравнение |x+3|-|x-5|=8 будет х≥5
-|x+3|+|x-5|=8
{x+3≥0
{-(x+3)+|x-5|=8
{x≥-3
{-x-3+|x-5|=8
{x≥-3 {x≥5
{x-5≥0 ⇒ {-8=8 - решений нет!
{-x-5+x-5=8
{x≥-3 { -3≤x<5
{x-5<0 ⇒ {x=-3 ⇒ x=-3
{-x-3-x+5=8
{x<-3 {x<-3
{x-5≥0 ⇒ {x≥5 - решений нет
{x+3+x-5=8 {x=5
{x<-3 {x<5
{x-5<0 ⇒ {x<-5 ⇒ x<-3
{x+3-x+5=8 {8=8
Ответ: х любое для переменных х≥5,
х=-3
х-дюбое для переменных х<-3
Автор ответа:
0
//////////////////////////////////////////////////
Приложения:
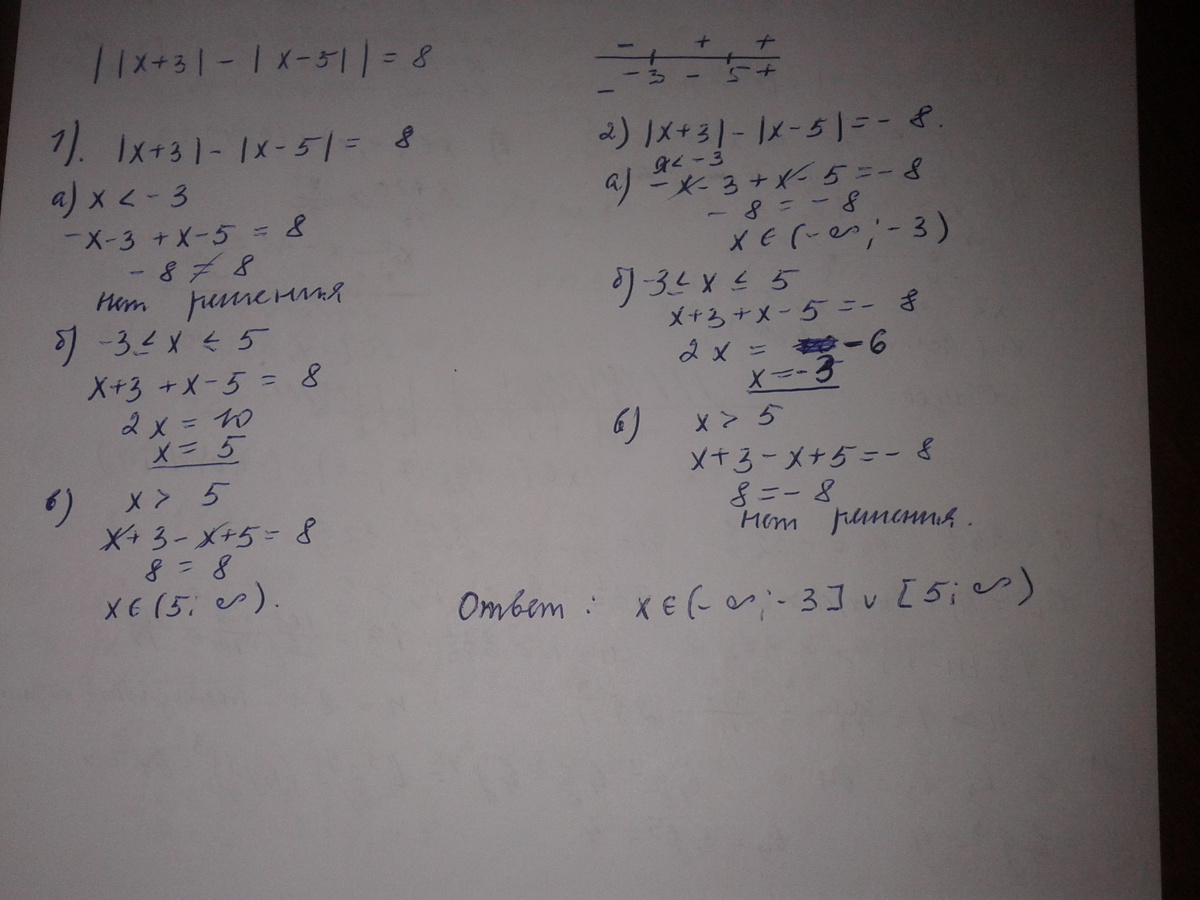
Похожие вопросы
Предмет: Физика,
автор: lollollollollollol49
Предмет: Алгебра,
автор: lozickayaelena
Предмет: Обществознание,
автор: LaynPRO123
Предмет: Физика,
автор: Оболтусиха
Предмет: Математика,
автор: Granitlog