Question

Найдите объем тела, полученного при вращении вокруг оси абсцисс фигуры, ограниченной линиями y=Ix-1I, x=-1, x=2, y=0

Answer 1

y=Ix-1I, x=-1, x=2, y=0
+
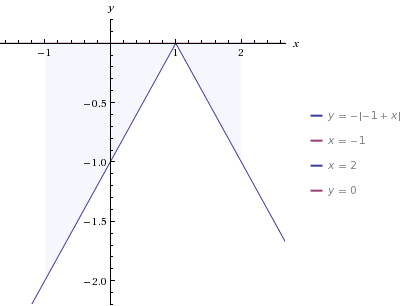
y=-Ix-1I, x=-1, x=2, y=0

$intlimits^2_{-1} {|-1+x|} , dx + intlimits^2_{-1} {|-1+x|} , dx = frac{5}{2} +frac{5}{2}=5$ кв.ед.

Answer 2

Если функция линейная, то можно объём определить без интеграла.
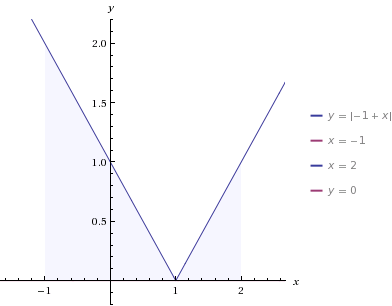
График функции y=Ix-1I - это ломаная линия, идущая от точки (-1, 2) вниз до точки (1, 0) и вверх до (2,1)
Если считать, что запись "Найдите объем тела, полученного при вращении вокруг оси абсцисс фигуры, ограниченной линией y=0" означает, что нужно определить только половину фигуры, то это будет половины двух конусов:
- радиус основания большего конуса 2, высота - 2,
- радиус основания меньшего конуса 1, высота - 1
V = S*H/3 = πR²H / 3 = π2²*2 /3 + π1²*1 / 3 =
 =8,3776+1,0472 = 9,4248.
Если разделить на 2, получим 4,7124 куб. ед.

Answer 3

Как получилось 5/2?