Question

через точку пересечения диагоналей параллелограмма проведена прямая. Докажите,что отрезок ещё, заключенный между параллельными сторонами, делится этой точкой пополам

Answer 1

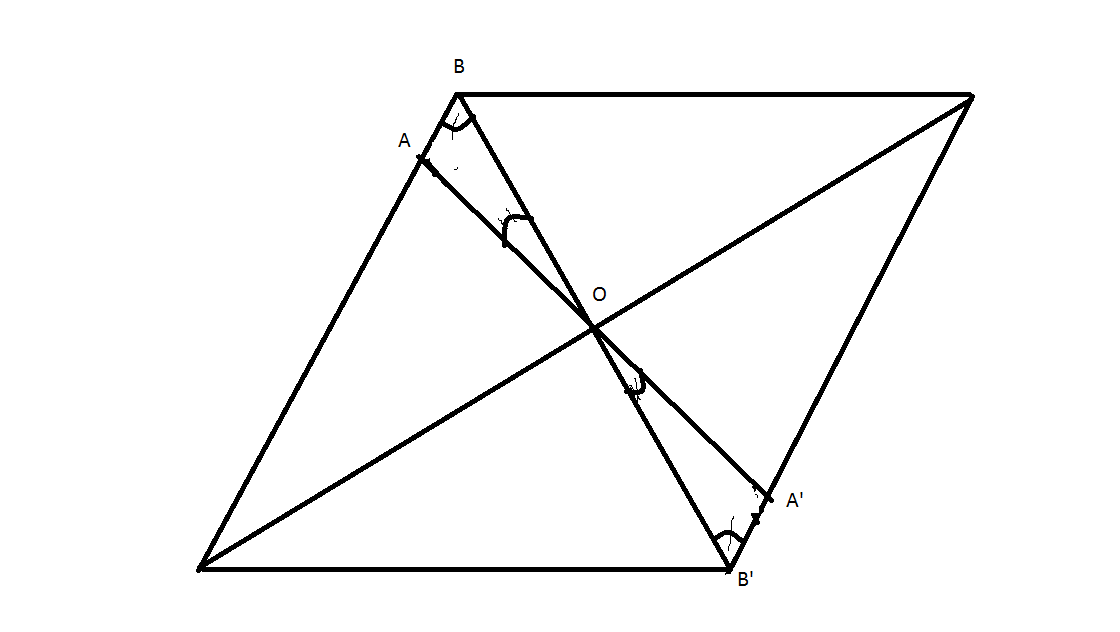
Углы  AOB=A'OB' как  вертикальные
Углы  OBA=OB'A' как внутренние  накрест лежащие,откуда тк  по  свойству диагоналей параллелограмма  BO=OB',то  треугольники AOB=A'OB' по  стороне и 2  прилежащим углам,откуда  AO=OA'
ЧТД.

Answer 2

спс

Answer 3

Через точку О пересечения диагоналей параллелограмма проведем произвольную прямую а, пересекающую параллельные стороны параллелограмма в точках M и N.
Треугольники АМО и CNO равны, так как АО=ОС (диагонали параллелограмма точкой пересечения делятся пополам), угол АОМ равен углу СОN (вертикальные), угол МАО равен углу NСО (внутренние накрест лежащие при параллельных прямых АВ и СD и секущей АС). Из равенства треугольников МО=ОN.
Что и требовалось доказать.

Answer 4

спс