Question

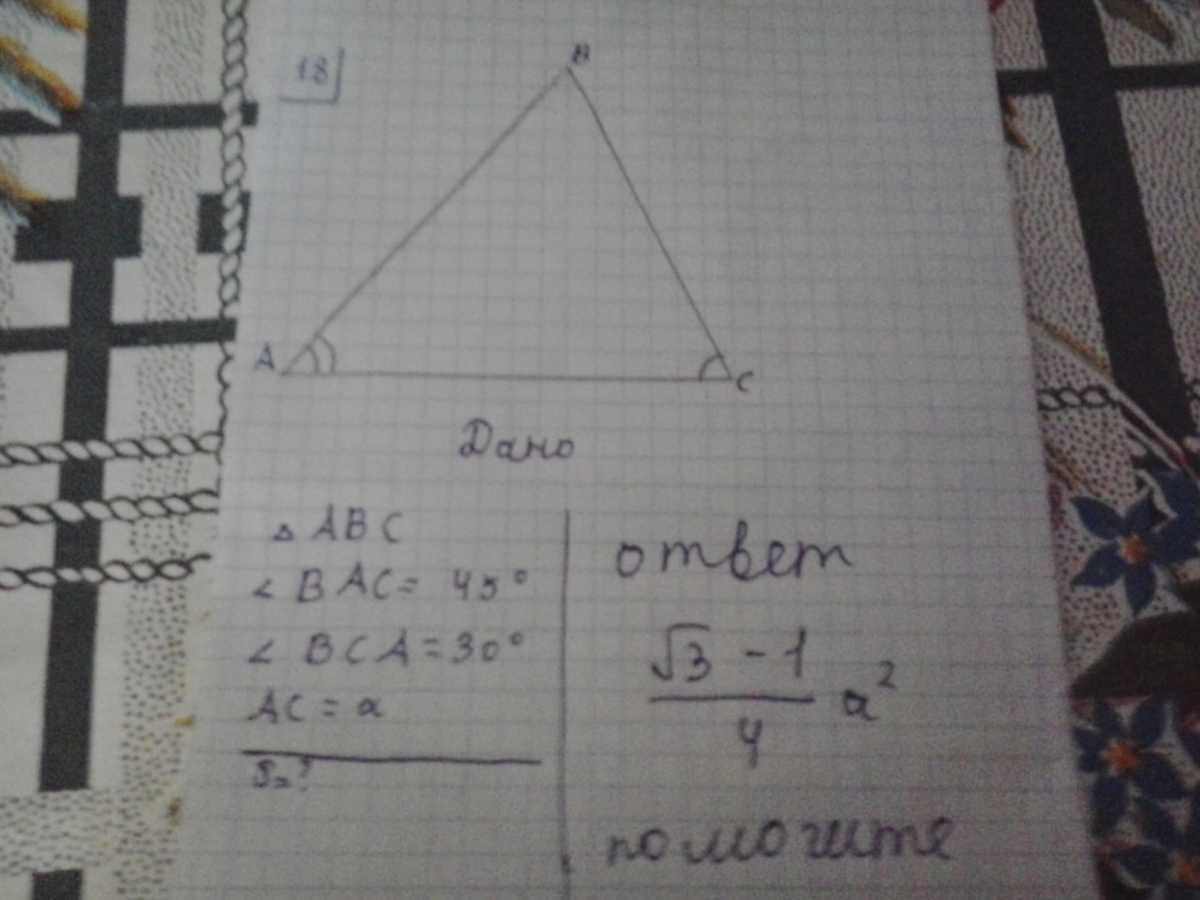
                                              ДАНО
треугольник ABC
<BAC=45°
<BCA=30°
AC=a
S=?

Answer 1

есть формула площади
S=1/2·a^2·sin(45)sin(30)/sin(180-45-30)
S=1/2·a^2(корень из 2/2 *1/2/)/sin (60+45))=1/2·a^2(корень из 2/2 *1/2/)/sin60*cos45+cos45*sin60 )=1/2·a^2(корень из 2/2 *1/2/)/(корень из 3/2*корень из 2/2+корень из 2/2+1/2)
корень из 22 сокращаем остается и 1/2 тоже сокращаем в числителе и знамнателе
1/2·a^2 (1/корень из 3 +1)
и числитель и знаменатель умножаем на корень из 3-1 и получаем ваш ответ

Answer 2

Угол В=180⁰-45⁹-30⁹=105⁰
По теореме синусов:

$frac{a}{sin alpha } = frac{b}{sin beta }= frac{c}{singamma} =2R$

В данном треугольнике:

$frac{a}{sin 105 ^{o} } = frac{BC}{sin 45 ^{o} }Rightarrow BC= frac{acdot sin 45 ^{o} }{sin 105 ^{o} }$

sin 105°=sin 75°=sin(45°+30°)=sin 45°cos30°+cos45°sin 30°=√2/2(√3/2+1/2)=(√6+√2)/4
тогда ВС=а:(√3+1)/2=2a/(√3+1)=а(√3-1) Освободились от иррациональности в знаменателе. Умножили и числитель и знаменатель на (√3-1) в знаменателе получили формулу разности квадратов  (√3)²-1=2.

Площадь треугольника можно найти по формуле

S=1/2·АС·ВС ·sin 30⁰=1/4·а·а·(√3-1)=а²(√3-1)/4