Предмет: Геометрия,
автор: Ejik17
На прямой содержащей медиану ad прямоугольного треугольника abc с прямым углом. C взята точка e удаленая от вершины a. На расстояние равное 4 ,найти площадь треугольника. bce, если bc -6 , ac-4
Ответы
Автор ответа:
0
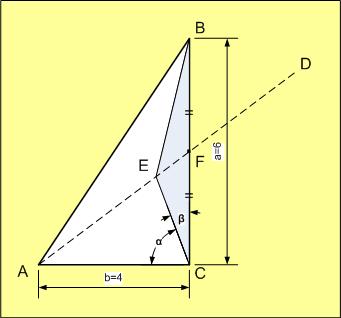
Рассматриваем прямоугольный ΔAFC. В нем катет AC=4 по условию, катет FC= (как половина ВС, поскольку AF - медиана. Гипотенуза AF может быть найдена по теореме Пифагора, но поскольку катеты равны 3 и 4, то это случай "египетского треугольника" (соотношение сторон 3:4:5) и можно без вычислений сказать, что его гипотенуза равна 5.
Тогда cos(FAC)=AC/AF=4/5=0.8, sin(FAC)=FC/AF=3/5=0.6.
Теперь рассмотрим ΔAEC. По условию EF=1 ⇒ AE=AF-EF=5-1=4.
По теореме косинусов EC²=AE²+AC²-2*AE*AC*cos(EAC)=4²+4²-2*4*4*0.8=16+16-25.6=6.4 ⇒ EC=√(6.4)≈2.53.
По теореме синусов EC/sin(EAC)=AE/sin(α) ⇒ sin(α)=AE*sin(EAC)/EC=4*0.6/√(6.4)=2.4/√(6.4).
Угол АСВ - прямой, поэтому угол β=π/2-α.
sin(β)=sin(π/2-a)=cos(α)=√(1-sin²α)=√(1-2.4²/6.4)=√(0.1)
Площадь ΔBCE=(1/2)*EC*BC*sin(β)=(1/2)*√(6.4)*6*√(0.1)=3√(0.64)=3*0.8=2.4 (ед²)
Тогда cos(FAC)=AC/AF=4/5=0.8, sin(FAC)=FC/AF=3/5=0.6.
Теперь рассмотрим ΔAEC. По условию EF=1 ⇒ AE=AF-EF=5-1=4.
По теореме косинусов EC²=AE²+AC²-2*AE*AC*cos(EAC)=4²+4²-2*4*4*0.8=16+16-25.6=6.4 ⇒ EC=√(6.4)≈2.53.
По теореме синусов EC/sin(EAC)=AE/sin(α) ⇒ sin(α)=AE*sin(EAC)/EC=4*0.6/√(6.4)=2.4/√(6.4).
Угол АСВ - прямой, поэтому угол β=π/2-α.
sin(β)=sin(π/2-a)=cos(α)=√(1-sin²α)=√(1-2.4²/6.4)=√(0.1)
Площадь ΔBCE=(1/2)*EC*BC*sin(β)=(1/2)*√(6.4)*6*√(0.1)=3√(0.64)=3*0.8=2.4 (ед²)
Приложения:
Автор ответа:
0
Ваше решение великолепно.Точность и предельно ясное решение
Похожие вопросы
Предмет: Математика,
автор: meerimmeka02
Предмет: Русский язык,
автор: Antonsychyov
Предмет: Математика,
автор: ajdynkyzyaaulym0
Предмет: Биология,
автор: Артур9559