Предмет: Геометрия,
автор: okBro
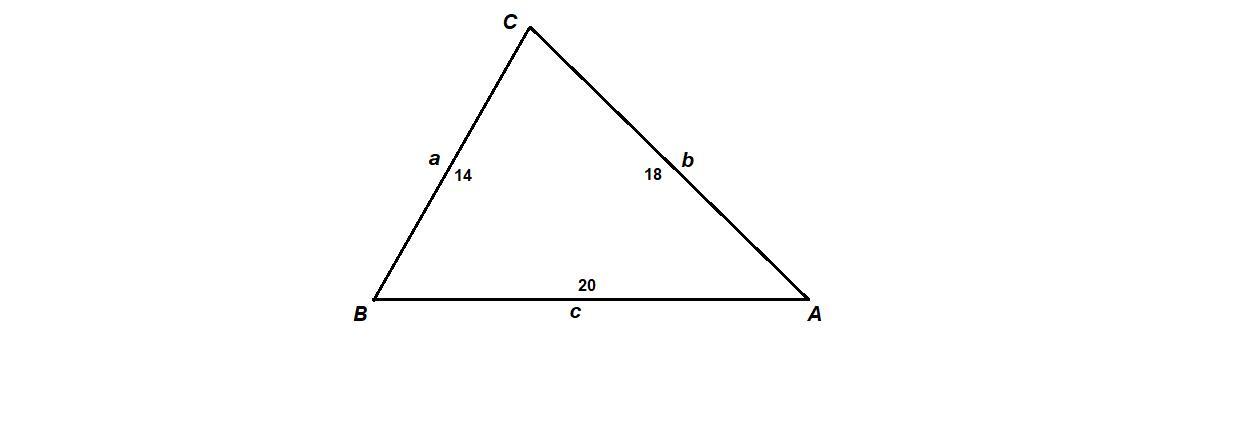
В треугольнике abc сторона а=14 см, б=18 см, с=20 см. найдите углы треугольника.
Ответы
Автор ответа:
0
Решается по теореме косинусов:
a2 = b2 + c2 - 2bc*Cos(A)
Cos(A) = (b2 + c2 - a2)/ (2bc)
Угол А = 43
Угол B = 61
Угол C = 76
Автор ответа:
0
Ответ: 43°, 61°, 76°
Объяснение:
a = 14 см
b = 18 см
c = 20 см
По теореме косинусов:
c² = a² + b² - 2ab · cosC
cosC = (a² + b² - c²) / (2ab)
cosC = (196 + 324 - 400) / (2 · 14 · 18) = 120 / (2 · 14 · 18) = 15/(7 · 9) = 5/21
cosC ≈ 0,2381
∠C ≈ 76°
Аналогично, находим угол А:
a² = b² + c² - 2bc · cosA
cosA = (b² + c² - a²) / (2bc)
cosA = (324 + 400 - 196) / (2 · 18 · 20) = 528 / 720 = 11/15
cos A ≈ 0,7333
∠A ≈ 43°
Сумма углов треугольника равна 180°.
∠B = 180° - (∠A + ∠C)
∠B ≈ 180° - (76° + 43°) ≈ 61°
Приложения:
Похожие вопросы
Предмет: Математика,
автор: shahurinaarina
Предмет: Русский язык,
автор: Ertugannurseitov
Предмет: Алгебра,
автор: jonix73
Предмет: Химия,
автор: Medina95
Предмет: География,
автор: rusakovwn