Question

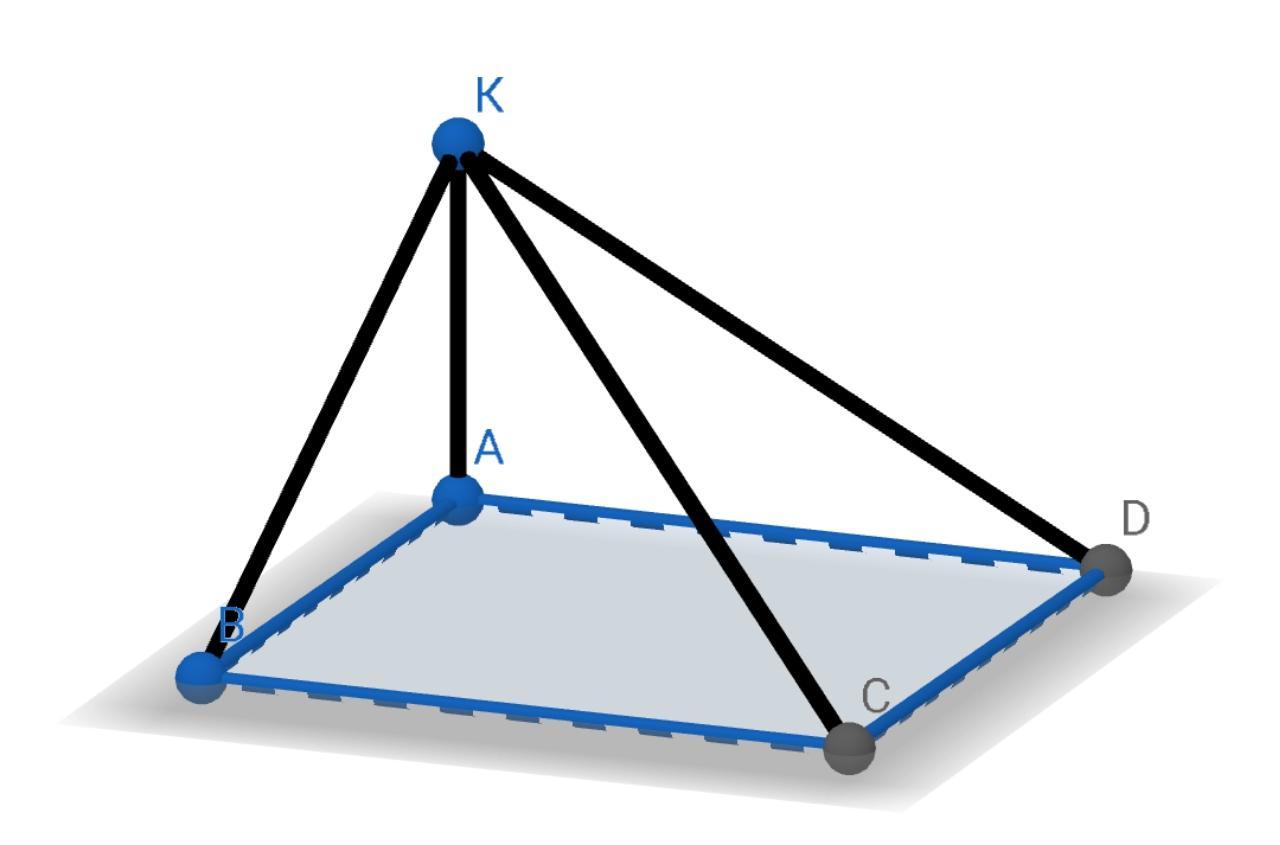
Из вершины A прямоугольника ABCD проведён к его плоскости перпендикуляр AK,конец которого отстоит от других вершин на расстоянии 6 см 7 см 9 см.Найти длину AK

Answer 1

Пусть АК = х см, тогда

AC^2 = 9^2 - x^2 = 81 - x^2 (поскольку угол KAC = 90°)

В треугольнике KAB AB^2 = 6^2 - x^2 = 36 - x^2.

Аналогично узнаем, что AD^2 = 49 - x^2.

И в плоскости основы AC^2 = AB^2 + AD^2

81 - x^2 = 49 - x^2 + 36 - x^2

x^2 = 4

x = +-2 = 2 (расстояние неотрицательное)

Ответ: 2 см