Предмет: Математика,
автор: nameisnull4
Найти производную, предварительно упростив аналитическое выражение функции
Приложения:
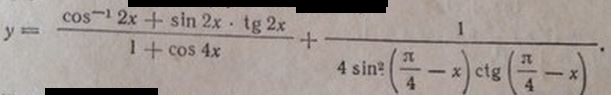
Ответы
Автор ответа:
0
y=1/cos³2x
y`=6sin2x/cos²2х
y=(1/cos2x + sin²2x/cos2x)/(1+cos4x) + 1/(4sin²(π/4-x)*cos(π/4-x)/sin(π/4 -x))=
=(1+sin²2x)/cos2x(1+cos4x) + 1/4sin(π/4-x)cos(π/4-x)=
=(1+sin²2x)/cos2x*2cos²2x + 1/2sin(π/2-2x)=
=(1+sin²2x/2cos³2x + 1/2cos2x= (1+sin²2x+cos²2x)/2cos³2x=2/2cos³2x=1/cos³2x
y`=(cos^-3 (2x)` *(cos2x)` *(2x)`=-3cos^-2(2x) *(-sin2x) *2=6sin2x/cos²2x
y`=6sin2x/cos²2х
y=(1/cos2x + sin²2x/cos2x)/(1+cos4x) + 1/(4sin²(π/4-x)*cos(π/4-x)/sin(π/4 -x))=
=(1+sin²2x)/cos2x(1+cos4x) + 1/4sin(π/4-x)cos(π/4-x)=
=(1+sin²2x)/cos2x*2cos²2x + 1/2sin(π/2-2x)=
=(1+sin²2x/2cos³2x + 1/2cos2x= (1+sin²2x+cos²2x)/2cos³2x=2/2cos³2x=1/cos³2x
y`=(cos^-3 (2x)` *(cos2x)` *(2x)`=-3cos^-2(2x) *(-sin2x) *2=6sin2x/cos²2x
Автор ответа:
0
а можно объяснить как получилось y=1/cos³2x ? если не сложно
Автор ответа:
0
Cложно, но можно.
Автор ответа:
0
Смотри.
Автор ответа:
0
Спасибо огромное
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: История,
автор: burenkop
Предмет: Музыка,
автор: insarseitkhan
Предмет: История,
автор: cherry1204
Предмет: Химия,
автор: platonovadasha