Предмет: Геометрия,
автор: лицеист1568
В треугольнике АВС угол АСВ тупой, ВО перпендикулярно АС,
OF перпендикулярно АВ, OD перпендикулярно ВС. Докажите, что угол АСВ равен углу DFB.
51 балл даю, я на Вас надеюсь!!!!!!!!!!
Ответы
Автор ответа:
0
Ну да, сложнейшая задача :(((
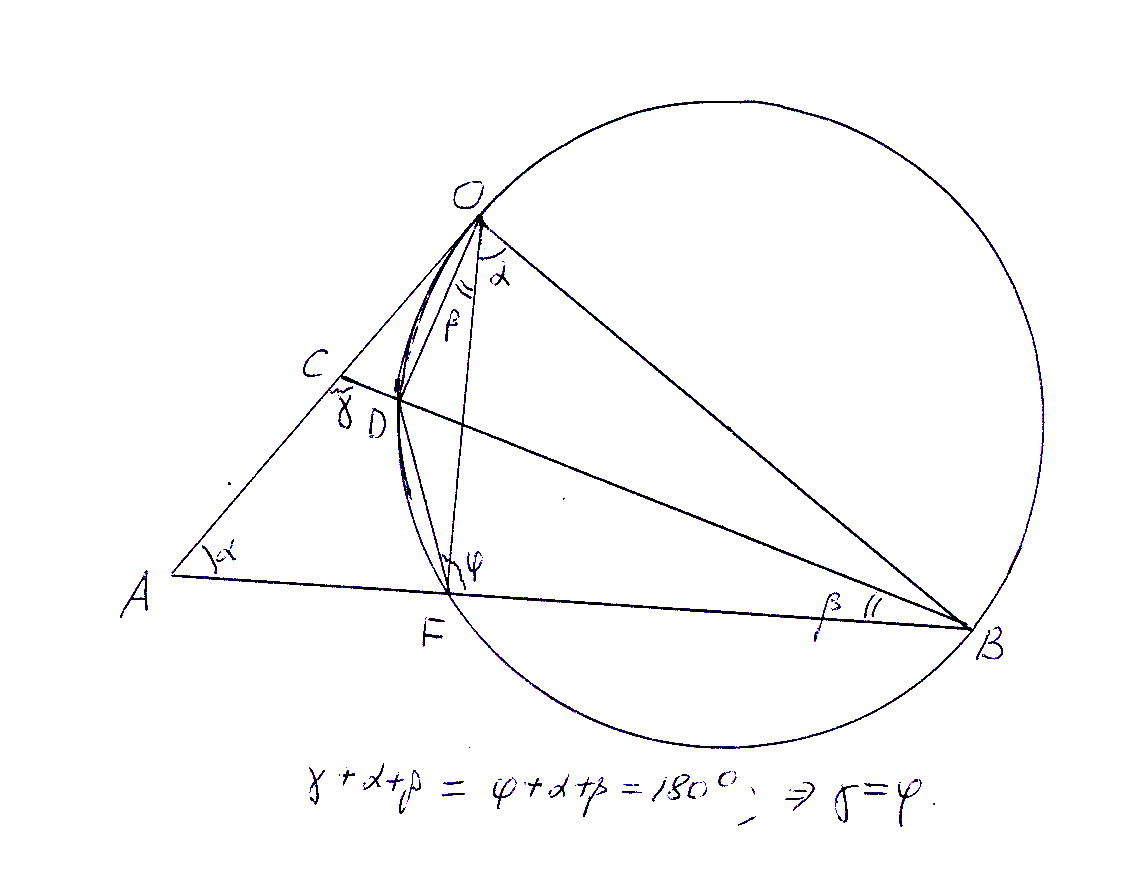
Углы ODB и OFB прямые, поэтому можно построить окружность на OB, как на диаметре, и при этом точки D и F лежат на этой окружности. То есть четырехугольник ODFB - вписанный в окружность.
Дальше, из прямоугольного треугольника AOB угол ABO = 90° - угол CAB;
поэтому угол CBO = 90° - угол CAB - угол CBA;
из прямоугольного треугольника ODB угол DOB = 90° - угол CBO;
угол DOB = угол CAB + угол CBA;
поскольку ODFB можно вписать в окружность, сумма углов DFB и DOB равна 180°;
То есть угол DFB = 180° - (угол CAB + угол CBA) = угол ACB; чтд.
PS. для любителей точных и минимальных решений - с углами можно разобраться на много проще. Вот так:
угол DOF = угол CBA, так как их стороны перпендикулярны (попарно).
По той же причине угол FOB = угол CAB.
То есть угол DOB = угол CAB + угол CBA;
PPS. угол DOF = угол CBA это так же сразу видно из того, что эти вписанные углы опираются на одну дугу DF построенной окружности.
На самом деле и для второй пары углов тоже есть возможность доказать равенство угол FOB = угол CAB, через дуги построенной окружности - дело в том, что AO - касательная к этой окружности, и угол AOF измеряется половиной дуги OF, так же как и угол OBA, а каждый из этих углов дополняет угол из пары (угол FOB и угол CAB) до 90°. То есть угол OBA = угол AOF; а угол FOB = 90° - угол OBA; угол CAB = 90° - угол AOF; => угол FOB = угол CAB;
Но это уже больше - для развлечения :)))
Углы ODB и OFB прямые, поэтому можно построить окружность на OB, как на диаметре, и при этом точки D и F лежат на этой окружности. То есть четырехугольник ODFB - вписанный в окружность.
Дальше, из прямоугольного треугольника AOB угол ABO = 90° - угол CAB;
поэтому угол CBO = 90° - угол CAB - угол CBA;
из прямоугольного треугольника ODB угол DOB = 90° - угол CBO;
угол DOB = угол CAB + угол CBA;
поскольку ODFB можно вписать в окружность, сумма углов DFB и DOB равна 180°;
То есть угол DFB = 180° - (угол CAB + угол CBA) = угол ACB; чтд.
PS. для любителей точных и минимальных решений - с углами можно разобраться на много проще. Вот так:
угол DOF = угол CBA, так как их стороны перпендикулярны (попарно).
По той же причине угол FOB = угол CAB.
То есть угол DOB = угол CAB + угол CBA;
PPS. угол DOF = угол CBA это так же сразу видно из того, что эти вписанные углы опираются на одну дугу DF построенной окружности.
На самом деле и для второй пары углов тоже есть возможность доказать равенство угол FOB = угол CAB, через дуги построенной окружности - дело в том, что AO - касательная к этой окружности, и угол AOF измеряется половиной дуги OF, так же как и угол OBA, а каждый из этих углов дополняет угол из пары (угол FOB и угол CAB) до 90°. То есть угол OBA = угол AOF; а угол FOB = 90° - угол OBA; угол CAB = 90° - угол AOF; => угол FOB = угол CAB;
Но это уже больше - для развлечения :)))
Приложения:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: Аноним
Предмет: Литература,
автор: sirena89
Предмет: Математика,
автор: lqhj553
Предмет: Математика,
автор: НастёнкаСЛ
Предмет: Алгебра,
автор: PANDA744