Question

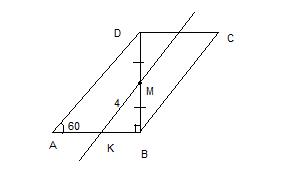
В Параллелограмме АВСД, угол А=60 градусов, диагональ ВД перпендикулярна к стороне АВ. Прямая, проходящая через середину отрезка ВД - точку М параллельно АД, пересекает сторону АВ в точке К, МК=4 см. Найдите площадь параллелограмма.

Answer 1

S=AB*BD
Рассмотрим прямоугольные треугольники ABD и KBM. Они подобны по первому признаку подобия: два угла одного треуг-ка соответственно равны двум углам другого. Угол ABD - общий прямой, а углы BAD и BKM равны как соответственные углы при пересечении параллельных прямых AD и КМ секущей АВ (<BKM=<A=60°).
Зная, что сумма острых углов прямоугольного треугольника равна 90°, находим угол ВМК:
<BMK=90-<BKM=90-60=30°.
Катет ВК прямоугольного треугольника KBM, лежащий против угла ВМК в 30°, равен половине гипотенузы МК, значит
ВК=4:2=2 см
По теореме Пифагора найдем ВМ:
BM=√MK²-BK²=√16-4=√12=2√3 см
У подобных треугольников ABD и KBM коэффициент подобия k равен:
k=BM : BD=1 : 2 (по условию М - середина отрезка BD). Значит,
BK : AB = 1 : 2, отсюда АВ = 2*ВК=2*2=4 см
BM : BD=1 : 2, отсюда BD = 2*BM=4√3 см
S=4*4√3=16√3 см²