Question

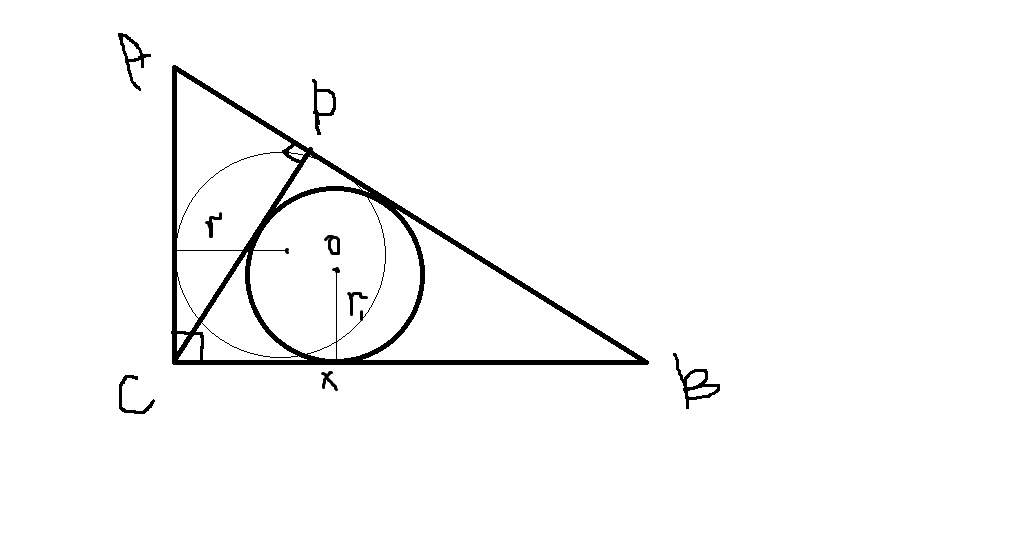
Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник ВCP, равен 60, тангенс угла ВАС равен 4/3. Найдите радиус вписанной окружности треугольника ABC.

___________________________
Заранее спасибо♡

Answer 1

1.Тангенс дает нам отношение сторон, т.к. tgВАС=4/3, значит сторона СВ так относится к стороне АС, как 4 к 3, по теореме Пифагора можно посчитать гипотенузу(она равна 5), следовательно треуг-к АВС является египетским (СА=3х, СВ=4х, АВ=5х)
2. Треуг-к АВС подобен треуг-ку СРВ(по двум углам), следовательно СРВ тоже египетский. Значит его стороны тоже относятся как 5:4:3.
Пусть у - одна часть, тогда СВ=5у, РВ=4у,СР=3у
Scpb= 1/2×3у×4у=6у²
Воспользуемся формулой радиуса вписаной окр-ти r1=2S/a+b+c, тогда 60=12у²/3у+4у+5у=у
След-но у=60
Сторона ВС=5у=5×60=300
3.Пусть в треуг-ке АВС х-одна часть, тогда СА=3х, СВ=4х, АВ=5х
ВС=4х=300
х=75
АС=3х=75×3=225
АВ=5х=75×5=375
Sabc=1/2×300×225=33750
r=2S/a+b+c= 2×33750/300+225+375=75
Ответ: 75