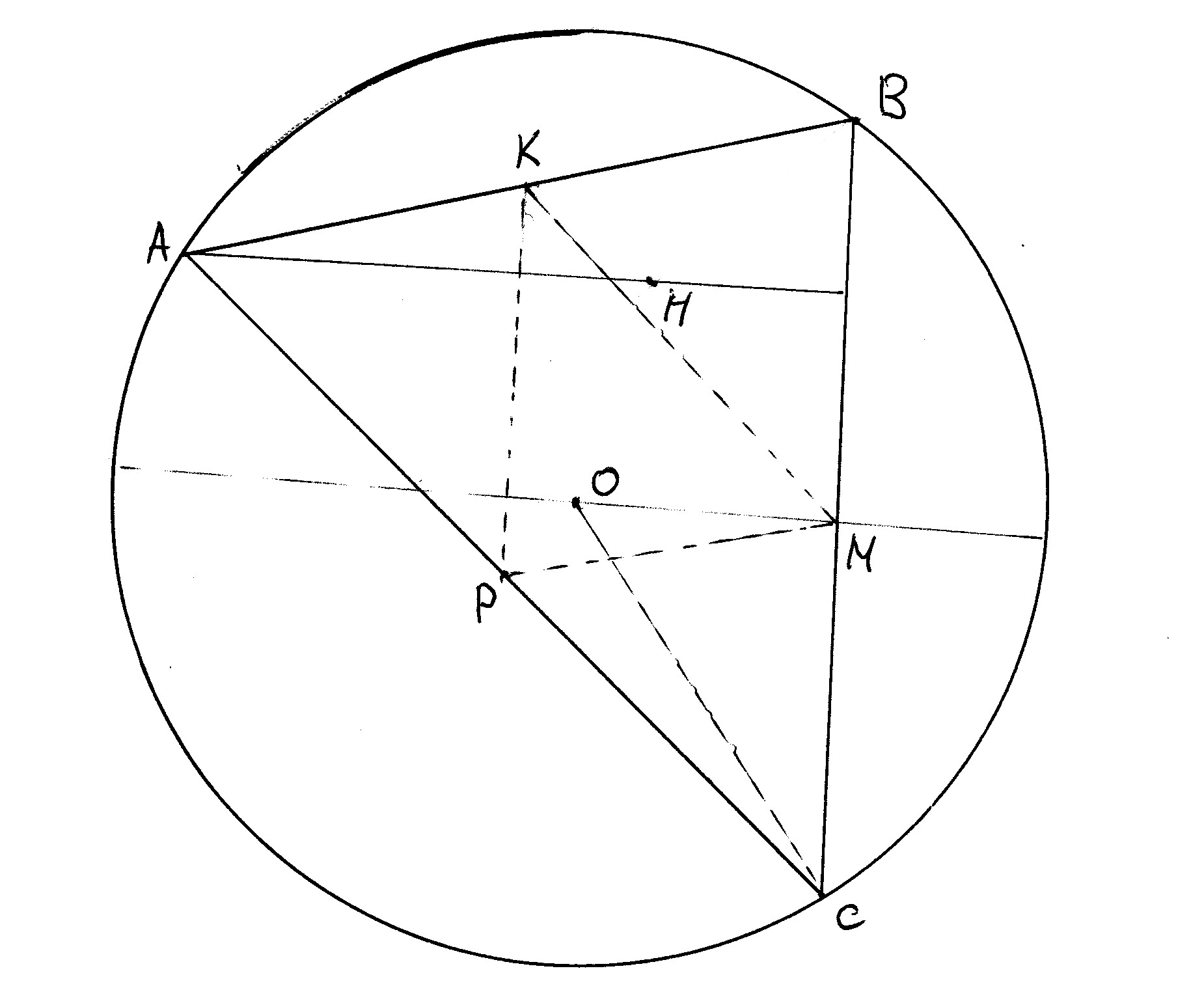
Найти угол треугольника, если расстояние от вершины этого угла до ортоцентра треугольника равна радиусу описаной окружности.
Ответы
надо же, я с трудом решил :))) побольше бы таких задач :))
Вот удивительно, сам по себе ортоцентр не играет никакой роли в решении. Для начала обратим внимание, что треугольник КРМ ( К, Р и М - середины сторон треугольника АВС) подобен треугольнику АВС. Центр О описанной вокруг АВС окружности лежит на пересечении медиатрис (перпендикуляров к сторонам в их серединах). Это означает, что О - точка пересечения высот треугольника КМР (каждая медиатриса АВС является высотой КМР). Таким образом, ОМ - расстояние от вершины до ортоцентра в треугольнике, у которого все размеры в два раза меньше, чем в АВС (конечно, и угол тот, который надо - угол КМР = угол ВАС).
Таким образом, (фактически по условию, вот оно - решение :)) ОМ = ОС/2.
Но это сразу означает, что угол МОС = 60 градусов. Поскольку ОВ симметрично ОС относительно ОМ (ну, М - середина ВС, ОМ перпендикулярно ВС), угол ВОМ тоже равен 60 градусов. Итак, угол ВОС = 120 градусов. Это центральный угол дуги ВС, на которую опирается искомый вписанный угол ВАС.
Ответ: угол ВАС = 60 градусов.