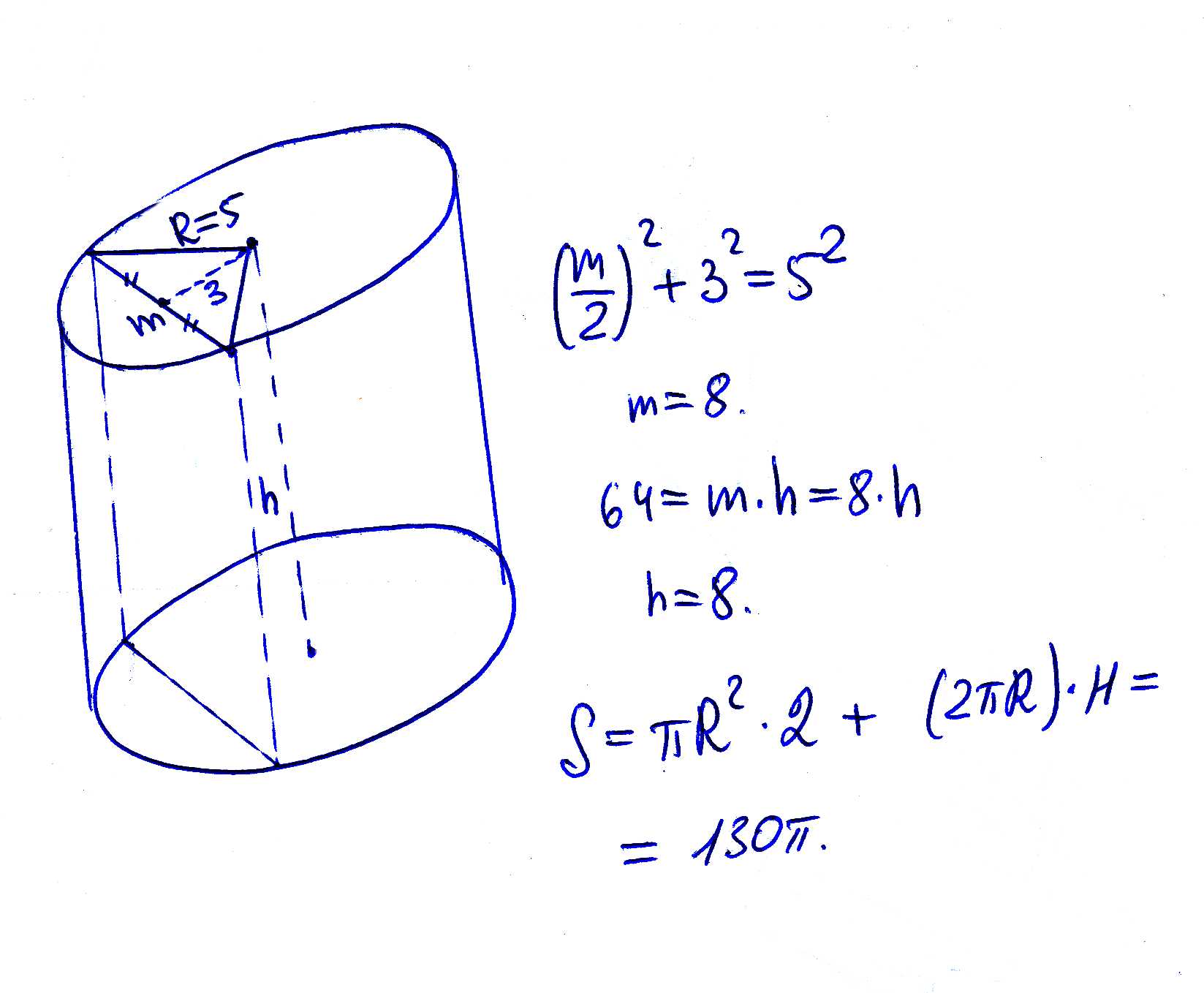
В цилиндре радиуса 5 см проведено паралельное оси сечение отстоящее от не) на росстояние 3 см. Найдите площадь полной поверхности цилиндра если площадь указанного сечения равна 64см в квадрате
Ответы
Для начала рассмотрим, что это за сечение. В основании цилиндра круг радиуса 5, сечение пересекает его по хорде, отстоящей от центра на 3. Половина длины хорды (пусть её длина m) и расстояние от центра связаны с радиусом круга теоремой Пифагора
(m/2)^2 + 3^2 = 5^2; откуда m = 8;
Обозначим высоту цилиндра h; ясно, что площадь сечения равна (ну, площадь прямоугольника, произведение сторон) m*h = 8*h = 64; h = 8;
Получилось, что заданное сечение - квадрат со стороной 8.
Осталось записать площадь полной поверхности и сосчитать.
Надо учесть, что площадь основания pi*5^2, и их - два. А площадь боковой поверхности равна длине окружности, умноженной на высоту цилиндра (это легко представить, как развертку :) - обернули цилиндр бумагой, а потом развернули на плоскости, получился прямоугольник со сторонами 2*pi*R, R=5, и h = 8)
2*(pi*5^2) + (2*pi*5)*8 = 130*pi;
Высоту цилиндра определим из площади вертикального сечения H=s/2a
В горизонтальной плоскости рассмотрим половину тр-ка образованного хордой и радиусами, из него а = √R²-3²=√(25-9)=4, H=64/(2*4)=8 cм
Sосн = пR² = 25π
Sбок = 2пRH = 80π
S = 2*Sосн + Sбок = 2*25π + 80π = 130π см²
