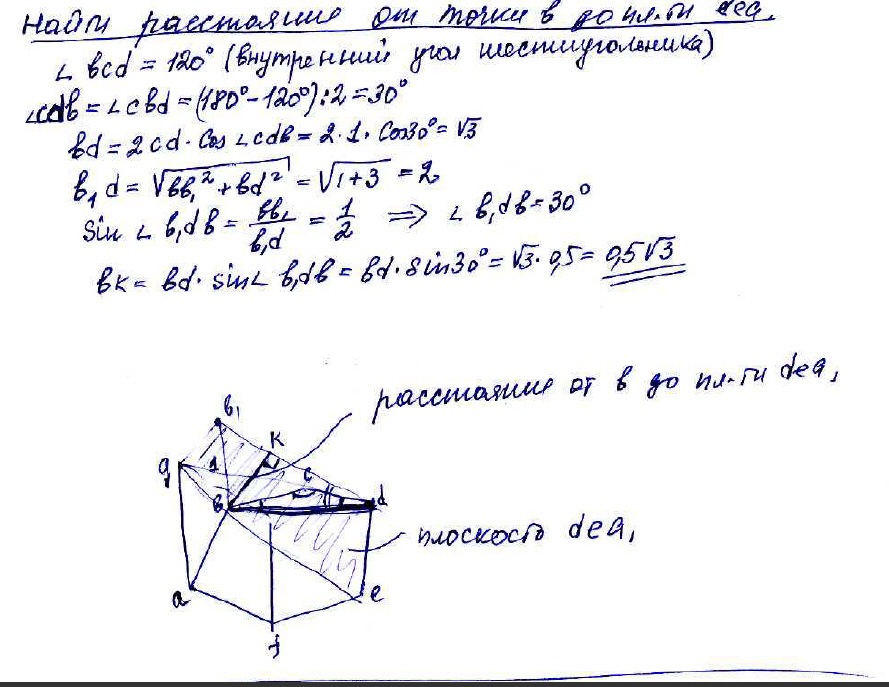
в прямоугольной шестиугольной призме abcdefa1b1c1d1e1f1 все ребра равны 1.найти расстояние от точки b до плоскости dea1
Ответы
Дано: ABC...D1E1F1 - правильная шестиугольная призма
все рёбра = а = 1
Найти: BH
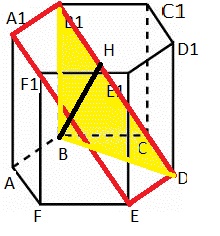
Решение: Расстояние от точки до плоскости измеряется длиной перпендикуляра, поэтому рассмотрим плоскость А1В1DE (на рис. выделена красным). Прямая В1D лежит в этой плоскости, следовательно, расстояние от точки В до плоскости равно расстоянию от точки В до прямой В1D. Проведём к этой прямой перпендикуляр ВН, а также соединим точки В и D.
Так как призма правильная по условию, значит боковые рёбра перпендикулярны плоскостям оснований, а значит угол В1ВD=90 градусов.
ВD - меньшая диагональ основания. Так как призма правильная, значит в основании лежит правильный шестиугольник (гексагон), а по свойству гексагона меньшая диагональ гексагона в sqrt(3) раз больше его стороны. Значит ВD=a*sqrt(3)=1*sqrt(3)=sqrt(3).
Рассмотрим прямоугольный треугольник ВВ1D (на рис. выделен жёлтым), в нём ВВ1=1, BD=sqrt(3), а по теореме Пифагора DB1=2.
ВН является высотой этого треугольника, а т.к. треугольник прямоугольный, то его высота вычислится по формуле BH=(BB1*BD)/B1D=sqrt(3)/2
Ответ: sqrt(3)/2
решение смотри во вложении.