Предмет: Геометрия,
автор: joker158
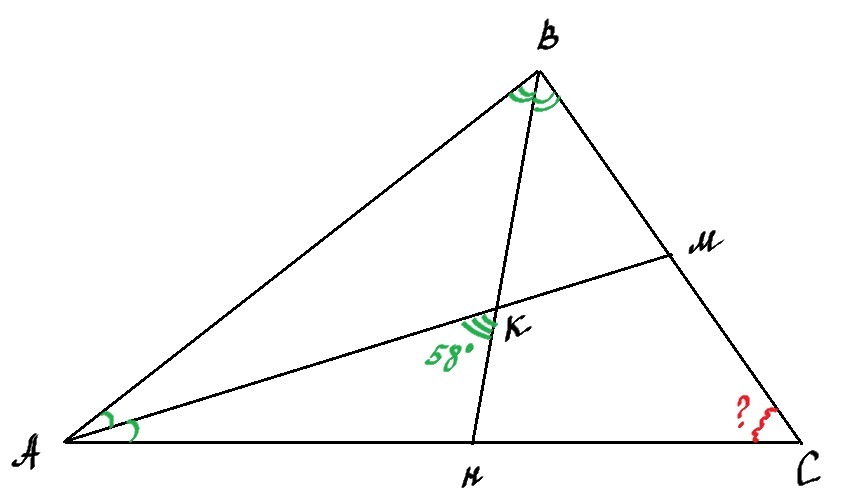
В треугольнике АВС проведены биссекктрисы АМ и ВН, пересекающиеся в точке К, причем угол АКНравен 58 градусов. Найдите угол АСВ.
Ответы
Автор ответа:
0
Рисунок в прикрепленном файле.
Рассмотрим ΔАВК. ∠АКН является внешним углом ΔАВК. Внешний угол треугольника равен сумме двух внутренних углов треугольника не смежных с ним, т.е. ∠АКН = ∠ВАК+∠АВК = 58°.
В ΔАВС ∠ВАС=2×∠ВАК, т.к. АК - биссектриса, ∠АВС=2×∠АВК, т.к. ВК - биссектриса.
∠ВАС+∠АВС=2×∠ВАК+2×∠АВК=2(∠ВАК+∠АВК)=2×58°=116°.
∠АСВ=180°-(∠ВАС+∠АВС)=180°-116°=64°.
Ответ: ∠АСВ = 64°.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: ivan27102007ivan
Предмет: География,
автор: ulanarepenkova
Предмет: Информатика,
автор: liliyaabramova1987
Предмет: Алгебра,
автор: krist94