Question

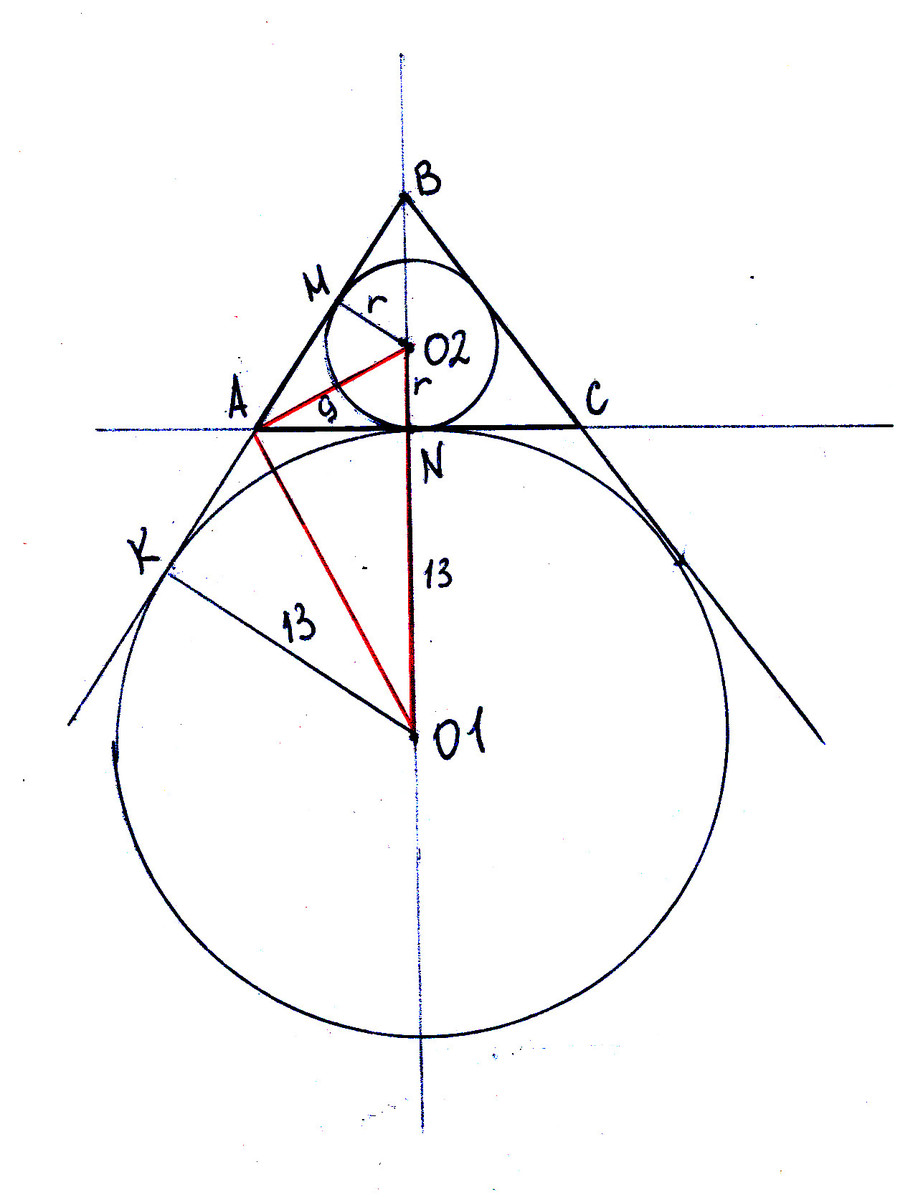
Основание AC равнобедренного треугольника ABC равно 18. Окружность радиуса 13 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC

Answer 1

Все обозначения на чертеже. АО1 перпендикулярно АО2, поскольку это - биссектрисы смежных углов. Поэтому АМ - высота в прямоугольном треугольнике АО1О2, и треугольники АМО1 и АМО2 подобны. а - основание, a = 18; R - радиус окружности с центром в О1, R = 13; r - радиус вписанной окружности.

О2А/АМ = АМ/О1А; r/(a/2) = (a/2)/R; r = (a/2)^2/R = 9^2/13 = 81/13.