Question

ПОМОГИТЕ ПОЖАЛУЙСТА, ОЧЕНЬ СРОЧНО!
В выпуклом четырехугольнике ABCD углы CDB и CAB равны. Докажите, что углы BCA иBDA также равны.

Answer 1

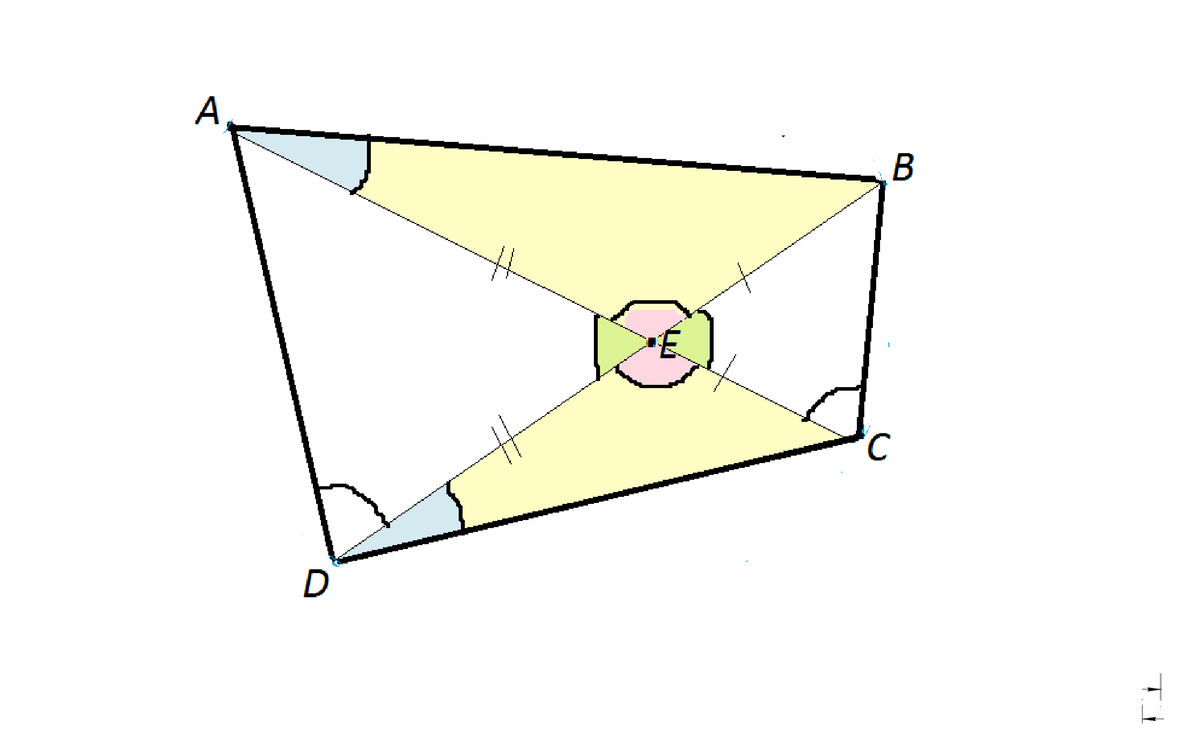
Проведем диагонали АС и ВD.Точку пересечения обозначим Е.
В треугольниках АВЕ и СDЕ имеется по два равных угла: один - по условию, второй - вертикальный. 
Первый признак подобия треугольников:
Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.⇒
∆ АВЕ ≈ ∆ СDЕ, ⇒
АЕ пропорциональна DE, ВЕ пропорциональна ЕС. 
В треугольниках ADE и ВСЕ:
АЕ пропорциональна DЕ, ВЕ- пропорциональна СЕ, углы АЕD и BEC равны, как вертикальные.
Второй признак подобия треугольников
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.
Треугольники ADE и ВСЕ подобны и углы, противолежащие пропорциональным сторонам, равны. ⇒∠ВDA=∠BCA
-----
[email protected]