Предмет: Алгебра,
автор: Shckolnik
Помогите решить:
Найдите наименьшее и наибольшее значения функции:
a) y=-2x^3 + 36x^2 - 66x + 1 на отрезке [-2;2]
б) y=1/2 cos2x + sinx на отрезке [0;п/2]
Ответы
Автор ответа:
0
РЕШЕНИЕ
Экстремумы находим по корням первой производной.
1.
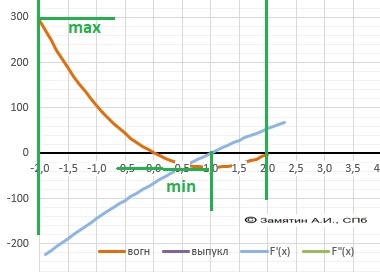
Y(x) = -2*x³ + 36*x² - 66*x+1 - функция
Y'(x) = - 6*x² + 72*x - 66 - первая производная.
Находим корни - решаем - D = 3600, x1 = 1, x2 = 11.
Делаем вывод - в области определения только один корень.
Вычисляем при Х = 1.
Ymin(1) = -2+36-66+1 = - 31 - минимум - ОТВЕТ
Функция с отрицательным коэффициентом при Х³ - убывает.
Значит максимум на границе - при Х = - 2
Вычисляем при Х = - 2
Ymax(-2) = 16+144+132+1 = 293 - максимум - ОТВЕТ
Рисунок к задаче в приложении.
2.
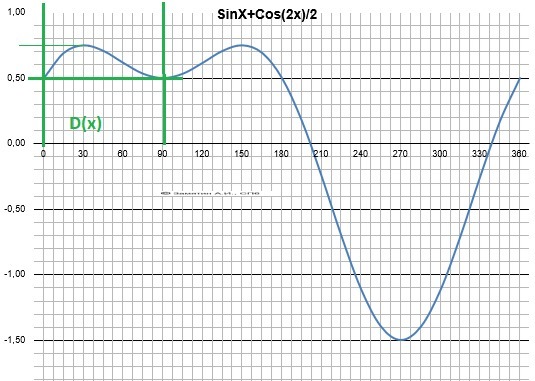
D(x) = [0;π/2] - область определения
Y(x) = sin(X) + 1/2*cos(X) - функция.
График функции - в приложении.
Y'(x) = cos(X) - sin(2*x) - производная.
Решаем уравнение
cos(x) - 2*sin(x)*cos(x) = 0
cos(x)*(1 - 2*sin(x)) = 0
x1 = π/6, x2 = 0.
Минимум при Х=0, Ymin(0) = 0.5 - ОТВЕТ
Максимум при Х = π/6 = 30°, Ymax(π/6) = 0.75 - ОТВЕТ
Экстремумы находим по корням первой производной.
1.
Y(x) = -2*x³ + 36*x² - 66*x+1 - функция
Y'(x) = - 6*x² + 72*x - 66 - первая производная.
Находим корни - решаем - D = 3600, x1 = 1, x2 = 11.
Делаем вывод - в области определения только один корень.
Вычисляем при Х = 1.
Ymin(1) = -2+36-66+1 = - 31 - минимум - ОТВЕТ
Функция с отрицательным коэффициентом при Х³ - убывает.
Значит максимум на границе - при Х = - 2
Вычисляем при Х = - 2
Ymax(-2) = 16+144+132+1 = 293 - максимум - ОТВЕТ
Рисунок к задаче в приложении.
2.
D(x) = [0;π/2] - область определения
Y(x) = sin(X) + 1/2*cos(X) - функция.
График функции - в приложении.
Y'(x) = cos(X) - sin(2*x) - производная.
Решаем уравнение
cos(x) - 2*sin(x)*cos(x) = 0
cos(x)*(1 - 2*sin(x)) = 0
x1 = π/6, x2 = 0.
Минимум при Х=0, Ymin(0) = 0.5 - ОТВЕТ
Максимум при Х = π/6 = 30°, Ymax(π/6) = 0.75 - ОТВЕТ
Приложения:
Похожие вопросы
Предмет: Українська мова,
автор: Anadelli
Предмет: Химия,
автор: kirigaya1411
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: Настика09
Предмет: Математика,
автор: Netel